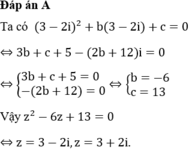Các câu hỏi tương tự
Cho phương trình
z
2
+
bz
+
c
0
b
,
c
∈
ℝ
có một nghiệm phức
z
3
-
2
i
. Nghiệm phức còn lại của phương trình là A.
3
+
2
i
B.
-
3
-
2
i...
Đọc tiếp
Cho phương trình z 2 + bz + c = 0 b , c ∈ ℝ có một nghiệm phức z = 3 - 2 i . Nghiệm phức còn lại của phương trình là
A. 3 + 2 i
B. - 3 - 2 i
C. - 3 + 2 i
D. 2 + 3 i
Biết rằng phương trình z 2 + bz + c = 0 (b,c∈R) có một nghiệm phức là z=1+2i. Khẳng định nào sau đây là đúng?
A. b+c= 0.
B. b+c= 2.
C. b+c= 3.
D. b+c=7.
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2i. Tích của hai số b và c bằng:
A. 3
B. -10
C. -2 và 5
D. 5
z
3
-
2
i
là nghiệm phức của phương trình nào trong các phương trình cho dưới đây? A.
x
2
–
x
+
3
-
i
0
B.
x
2
+
3
2
0
C.
x
2
+
x
+
3...
Đọc tiếp
z = 3 - 2 i là nghiệm phức của phương trình nào trong các phương trình cho dưới đây?
A. x 2 – x + 3 - i = 0
B. x 2 + 3 2 = 0
C. x 2 + x + 3 = 0
D. x 2 – x - 2 + 10 i = 0
Phương trình
z
2
+
az
+
b
0
,
a
,
b
∈
ℝ
có một nghiệm phức là
z
1
+
2
i
. Khi đó tổng
a
+
b
bằng A. -4 B. 3 C. 0 D. -3
Đọc tiếp
Phương trình z 2 + az + b = 0 , a , b ∈ ℝ có một nghiệm phức là z = 1 + 2 i . Khi đó tổng a + b bằng
A. -4
B. 3
C. 0
D. -3
Kí hiệu
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
2
i
Gọi M,N là các điểm biểu diễn của các số phức
z
1
,
z
2
Tính
z
2...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình z = 2 + 2 i Gọi M,N là các điểm biểu diễn của các số phức z 1 , z 2 Tính z = 2 + 2 i với O là gốc toạ độ.
A. T = 2 2 .
B. T = 2 2
C. T = 2 2 .
D. T = 2 2
Cho số phức z thỏa:
2
z
-
2
+
3
i
2
i
-
1
-
2
z
. Tập hợp điểm biểu diễn cho số phức z là một đường thẳng có phương trình là: A. 20x-16y-470 B. 20x+16y+470 C. 20x+32y-470 D. -20x+32y+470
Đọc tiếp
Cho số phức z thỏa: 2 z - 2 + 3 i = 2 i - 1 - 2 z . Tập hợp điểm biểu diễn cho số phức z là một đường thẳng có phương trình là:
A. 20x-16y-47=0
B. 20x+16y+47=0
C. 20x+32y-47=0
D. -20x+32y+47=0
Biết rằng phương trình
z
2
+
b
z
+
c
0
(
b
,
c
∈
R
)
có một nghiệm phức là
z
1
1
+
2
i
. Khi đó: A. b + c 2 B. b + c 3 C. b + c 0 D. b + c 7
Đọc tiếp
Biết rằng phương trình z 2 + b z + c = 0 ( b , c ∈ R ) có một nghiệm phức là z 1 = 1 + 2 i . Khi đó:
A. b + c = 2
B. b + c = 3
C. b + c = 0
D. b + c = 7
Biết số phức
z
1
1
+
i
v
à
z
2
là hai nghiệm của phương trình
z
2
+
b
z
+
c
0
(b,c là các số thực). Khi đó môdun của số phức
w
z
1
¯
−
2...
Đọc tiếp
Biết số phức z 1 = 1 + i v à z 2 là hai nghiệm của phương trình z 2 + b z + c = 0 (b,c là các số thực). Khi đó môdun của số phức w = z 1 ¯ − 2 i + 1 z 2 ¯ − 2 i + 1 là
A. w = 63 .
B. w = 65 .
C. w = 8.
D. w = 1.