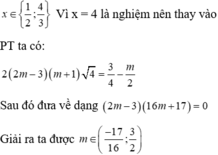Các câu hỏi tương tự
Cho phương trình: m2x + m(x - 3) = 6(x - 1) (m là tham số) (1)
a. Giải phương trình (1) khi m = 1
b. Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A=x^2+2x+3/x^2+2 đạt giá trị nhỏ nhất?
Cho phương trình: m2x + m(x - 3) = 6(x - 1) (m là tham số) (1)
a. Giải phương trình (1) khi m = 1
b. Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A=x^2+2x+3/x^2+2 đạt giá trị nhỏ nhất?
Cho phương trình 2 x + m = 3 x − 2 . Tìm giá trị của tham số m để phương trình có nghiệm x = 4.
Cho phương trình\(\left(m^2+2m+3\right)\cdot\left(x-6\right)=0.\)
(m là tham số)
a) Tìm giá trị của m để phương trình nhận x=2 là một nghiệm
b) Tìm giá trị của m để phương trình có nghiệm x duy nhất đạt giá trị lớn nhất
cho phương trình \(\frac{x^2}{16}-m=\frac{1}{2}\left(2m+1\right)\left(m-1\right)x\)
tìm giá trị tham số m để phương trình có nghiệm x=4
Cho phương trình x²-mx+m-1=0 (ẩn x, tham số m )
a)giải phương trình với m=3
b)chứng tỏ phường trình luôn có nghiệm với mọi giá trị m
c)gọi x₁ và x₂ là 2 nghiệm của phương trình . Tìm m để biểu thức A=x²₁ +x₂²-4x₁x₂ đạt giá trị nhỏ nhất. tìm giá trị nhỏ nhất đó
cho phương trình (2m-1 )/(x-1)= 2-m (m là tham số) . tìm giá trị vủa m để phương trình có nghiệm lớn hơn -1
Cho phương trình (ẩn x): (x – m)(x + 2) – 5mx + 4 = (x + m)(x – 2) – 6x (1).
Tìm các giá trị của m để phương trình (1) có nghiệm gấp đôi nghiệm của phương
trình 2x( x – 3 ) – 6x = 2(x – 1)(x + 5).
Cho phương trình x^2+(m-2)x-m13 (m là tham số). Tìm m để phương trình có nghiệm x 3. Khi đó, tìm nghiệm còn lại?
Đọc tiếp
Cho phương trình x^2+(m-2)x-m=13
(m là tham số).
Tìm m để phương trình có nghiệm x = 3. Khi đó, tìm nghiệm còn lại?
1) Giải phương trình: \(\left(2021x-2020\right)^3=8\left(x-1\right)^3+\left(2019x-2018\right)^3\)
2) Cho phương trình ẩn x: \(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\) , với m là tham số. Tìm tất cả các giá trị của tham số m để phương trình có nghiệm không âm.