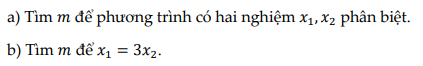a) \(x^2+2\left(m+1\right)x+m^2+2=0\left(1\right)\)
Để \(\left(1\right)\) có \(2\) nghiệm phân biệt \(x_1;x_2\) khi và chỉ khi
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-m^2-2>0\)
\(\Leftrightarrow2m-1>0\)
\(\Leftrightarrow m>\dfrac{1}{2}\)
b) Theo đề bài ta có : \(x_1=3x_2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4x_2=-2\left(m+1\right)\left(2\right)\\x_1.x_2=3x_2^2=m^2+2\left(3\right)\end{matrix}\right.\)
\(\left(2\right)\Rightarrow x_2=-\dfrac{m+1}{2}\)
\(\left(3\right)\Rightarrow3.\left(-\dfrac{m+1}{2}\right)^2=m^2+2\)
\(\Leftrightarrow3.\dfrac{\left(m^2+2m+1\right)}{4}=m^2+2\)
\(\Leftrightarrow m^2-6m+5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=5\end{matrix}\right.\) thỏa mãn \(m>\dfrac{1}{2}\)
Vậy với \(m\in\left\{1;5\right\}\) thỏa mãn đề bài