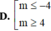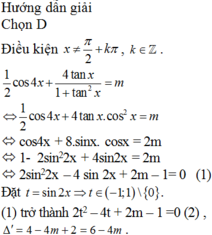
Ta xét (1) có nghiệm, tức là (2) có nghiệm t 0 ∈ - 1 ; 1

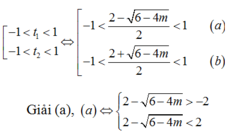
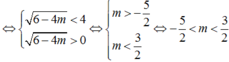
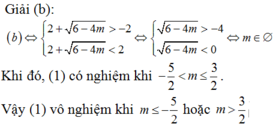
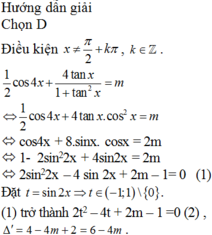
Ta xét (1) có nghiệm, tức là (2) có nghiệm t 0 ∈ - 1 ; 1

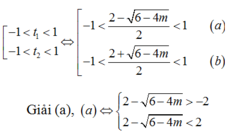
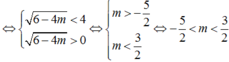
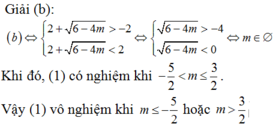
Cho phương trình 1 2 cos 4 x + 4 tan x 1 + tan 2 x = m . Để phương trình vô nghiệm, các giá trị của tham số m phải thỏa mãn điều kiện:
![]()
![]()
![]()
![]()
Cho phương trình 1 2 cos 4 x + 4 tanx 1 + tan 2 x = m . Để phương trình vô nghiệm, các giá trị của tham số m phải thỏa mãn điều kiện:
A. - 5 2 ≤ m ≤ 0
B. m > 1
C. 0 < m
D. m < - 5 2 hay m > 3 2 .
Tìm tất cả các giá trị thực của tham số m để phương trình 5 x 2 + 12 x + 16 = m ( x + 2 ) x 2 + 2 có hai nghiệm thực phân biệt thỏa mãn điều kiện 2017 2 x + x + 1 - 2017 2 x - x + 1 + 2018 x ≤ 2018
A. m ∈ ( 2 6 ; 3 3 ]
B. m ∈ [ 2 6 ; 3 3 ]
C. m ∈ ( 3 3 ; 11 3 3 ) ∪ { 2 6 }
D. m ∈ ( 2 6 ; 11 3 3 )
Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
Số các giá trị nguyên của m để phương trình ( cos x + 1).(4.cos 2x – m.cos x) = m.sin2x có đúng 2 nghiệm x ∈ 0 , 2 π 3 là:
A. 3.
B. 0.
C. 2.
D. 1.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + 2 cos x + 1 + 2 sin x = 1 2 m có nghiệm?
A. 3.
B. 5.
C. 4.
D. 2.
1) cho góc x thỏa mãn \(cosx=-\dfrac{4}{5}\) và \(\pi< x< \dfrac{3\pi}{2}\) tính \(P=tan\left(x-\dfrac{\pi}{4}\right)\)
2) giải phương trình \(2cosx-\sqrt{2}=0\)
3) phương trình lượng giác \(cos3x=cos\dfrac{\pi}{15}\) có nghiệm là
Điều kiện của tham số m để phương trình m.sin x – 3.cos x = 5 có nghiệm là
![]()
![]()
![]()