Xem E là ảnh của A qua phép quay tâm B, góc 90 ο . Khi A chạy trên nửa đường tròn (O), E sẽ chạy trên nửa đường tròn (O') là ảnh của nửa đường tròn (O) qua phép quay tâm tâm B, góc 90 ο .
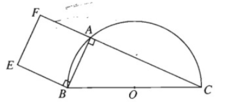
Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó.
Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ A G →
B. Phép vị tự tâm A tỉ số 2 3 .
C. Phép vị tự tâm M tỉ số 1 3
D. Phép tịnh tiến theo vectơ M G → .
Cho tam giác SAB vuông tại A, ABS= 60 o đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho △ S A B và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích V 1 , V 2 Khẳng định nào dưới đây đúng?
Cho 2 điểm phân biệt B,C cố định ( BC không phải là đường kính) trên đường tròn (O), điểm A di động trên (O), M là trung điểm BC, H là trực tâm tam giác ABC. Khi A di chuyển trên đường tròn (O) thì H di chuyển trên đường tròn (O;) là ảnh của (O) qua phép tịnh tiến theo u → . Khi đó bằng
A. B C →
B. O B →
C. 2 O M →
D. 2 O C →
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?
A. R 3
B. R 3 2
C. R 3 3
D. R 2
Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ^ và gọi H là hình chiếu vuông góc của C lên AB. Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất
A. α = 60 0
B. α = 45 0
C. α = a r c tan 1 2
D. α = 30 0
Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
