Các câu hỏi tương tự
Cho nửa đường tròn tâm o đường kính AB=4a (a>0). tính a theo diện tích mặt cầu và thể tích hình cầu tạo ra khi quay nửa đường (O) quay 1 vòng quanh đường kính AB cố định
cho nửa đường tròn tâm o đường kính AB=4a (a>0). tính a theo diện tích mặt cầu tạo ra khi quay nửa đường (O) quay 1 vòng quanh đường kính AB cố định
cho tam giác ABC vuông tại A có BC=2a; B = 300 và đường tròn (O) đường kính AB (như hình vẽ). Quay hình tròn (O) và tam giác ABC quanh cạnh AB cố định thì được một hình cầu và một hình nón. so sánh diện tích mặt cầu và diện tích toàn phần của hình nón
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Cho nửa đường tròn tâm O, đường kính AB 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại Na, Chứng minh các tam giác MON và APB đồng dạngb, Chứng minh AM.BN
R
2
c, Tính tỉ số
S
M
O
N...
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại N
a, Chứng minh các tam giác MON và APB đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn đường kính AB quay một vòng quanh AB sinh ra
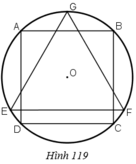
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
Cho nửa đường tròn tâm O, đường kính AB 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.a, Chứng minh MON và APB là hai tam giác vuông đồng dạngb, Chứng minh AM.BN
R
2
c, Tính tỉ số
S
M
O
N
S...
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a, Chứng minh MON và APB là hai tam giác vuông đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra
Cho nửa đường tròn tâm O đường kính AB. Ax, By vuông góc với AB tại A, B( Ax, By cùng thuộc 1 mặt phẳng bờ AB có chứa nửa đường tròn). Một góc zOt bằng 90 độ quay quanh O cắt Ax, By tại C và D. Chứng minh CD là tiếp tuyến của đường tròn (O).
Cho tam giác ABC vuông tại A có BC = 20, B = 30" và đường tròn (O) Qinmg kinh AE như hình vẽ. Quay đựng tròn (O) và tam giác ABC quanh cạnh AB cố định thì được một hình cầu và một linh tòa so sánh điều tích mặt cấu và diện tích toàn phần của hình nón.








