Các câu hỏi tương tự
cho tam giác ABC vuông tại A có BC=2a; B = 300 và đường tròn (O) đường kính AB (như hình vẽ). Quay hình tròn (O) và tam giác ABC quanh cạnh AB cố định thì được một hình cầu và một hình nón. so sánh diện tích mặt cầu và diện tích toàn phần của hình nón
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.Hình 119
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
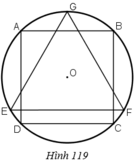
Hình 119
Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc A C B = 30 ° . Tính diện tích xung quanh và thể tích hình nón.
Quay tam giác vuông ABC ∠ A = 90 ° một vòng quanh cạnh AB là được một hình nón. Tính thể tích và diện tích xung quanh của hình nón đó biết BC = 12cm và ABC = 30 ° .
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh rab, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón
Đọc tiếp
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:
a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra
b, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón
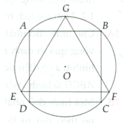
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
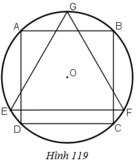
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Cho tam giác ABC vuông tại A có B = 30 0 và BC = 4 cm
a, Quay tam giác đó một vòng quanh cạnh AB. Hãy tính diện tích xung quanh và thể tích của hình tạo thành
b, Tính diện tích toàn phần của hình tạo thành
Câu 4 (3 điểm)1. Cho (O; R) cố định và điểm A thay đổi nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với (O) (với B, C là các tiếp điểm). Vẽ cát tuyến ADE với (O) (D nằm giữa A và E ; DE không đi qua O). Gọi H là giao điểm của AO và BC.a. Chứng minh rằng tứ giác ABOC nội tiếp đường tròn.b. Chứng minh rằng AH.AO AD.AE và tứ giác DEOH là tứ giác nội tiếp.c. Qua O vẽ đường thẳng vuông góc với AO cắt các tia AB, AC lần lượt tại M, N. Tìm vị trí của điểm A ở ngoài (O) để diện tích tam giác AMN đạt...
Đọc tiếp
Câu 4 (3 điểm)
1. Cho (O; R) cố định và điểm A thay đổi nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với (O) (với B, C là các tiếp điểm). Vẽ cát tuyến ADE với (O) (D nằm giữa A và E ; DE không đi qua O). Gọi H là giao điểm của AO và BC.
a. Chứng minh rằng tứ giác ABOC nội tiếp đường tròn.
b. Chứng minh rằng AH.AO = AD.AE và tứ giác DEOH là tứ giác nội tiếp.
c. Qua O vẽ đường thẳng vuông góc với AO cắt các tia AB, AC lần lượt tại M, N. Tìm vị trí của điểm A ở ngoài (O) để diện tích tam giác AMN đạt giá trị nhỏ nhất.
2. Một tam giác vuông có độ dài hai cạnh góc vuông là 2cm và 3cm. Quay tam giác vuông đó quanh cạnh góc vuông bé ta đtợc hình nón. Tính diện tích xunh quanh của hình nón đó.
Cho tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm . Quay một vòng quanh cạnh AB cố định ta được một hình nón có diện tích xung quanh là??






