Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
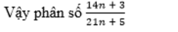 là phân số tối giản.
là phân số tối giản.
Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
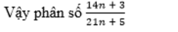 là phân số tối giản.
là phân số tối giản.
chứng minh rằng 21.n+4/14.n+3 là phân số tối giản (n thuộc N) ?
Cho n thuộc N, Chứng tỏ rằng phân số 14n+3/21n+5 là phân số tối giản.
Cho n thuộc N. Chứng tỏ rằng phân số: 14n+3/21n+5 là phân số tối giản
Cho n ∈ N. Chứng tỏ rằng phân số
14 n + 3 21 n + 5 là phân số tối giản
Cho n ∈ N . Chứng tỏ rằng phân số 14 n + 3 21 n + 5 là phân số tối giản
Chứng tỏ rằng mọi phân số có dạng :
\(\dfrac{2n+3}{3n+5}\) = ( n ∈ N ) đều là phân số tối giản .
Bài 1:
Chứng tỏ rằng mọi phân số có dạng n + 1 / 2n + 3 (n thuộc N) đều là phân số tối giản
Bài 2:
Chứng tỏ rằng mọi phân số có dạng 2n + 3 / 3n + 5 (n thuộc N) đều là phân số tối giản
Bài 3:
Cho góc mOx , tia Om nằm giữa hai tia Ox và Oy. Hãy chứng tỏ rằng:
a) Các góc mOx và mOy là các góc nhọn
b) Tia Ox không nằm giữa hai tia Om và Oy
Bài 1:
Chứng tỏ rằng mọi phân số có dạng n + 1 / 2n + 3 (n thuộc N) đều là phân số tối giản
Bài 2:
Chứng tỏ rằng mọi phân số có dạng 2n + 3 / 3n + 5 (n thuộc N) đều là phân số tối giản
Bài 3:
Cho góc mOx , tia Om nằm giữa hai tia Ox và Oy. Hãy chứng tỏ rằng:
a) Các góc mOx và mOy là các góc nhọn
b) Tia Ox không nằm giữa hai tia Om và Oy
Cho n thuộc N . Chứng tỏ rằng phân số 3n+5/8n + 13 là phân số tối giản