Các câu hỏi tương tự
Cho hình nón (N) có đường sinh tạo với đáy một góc
60
0
. Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N).
Đọc tiếp
Cho hình nón (N) có đường sinh tạo với đáy một góc 60 0 . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N).
![]()
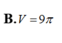
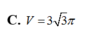
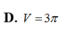
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng
(
α
)
qua tâm đáy và tạo với mặt đáy một góc
60
∘
tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng
(
α
)
?
Đọc tiếp
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng ( α ) qua tâm đáy và tạo với mặt đáy một góc 60 ∘ tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng ( α ) ?
![]()
![]()
![]()
![]()
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng
α
qua tâm đáy và tạo với mặt đáy một góc
60
°
tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng
α
?
Đọc tiếp
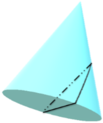
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng α qua tâm đáy và tạo với mặt đáy một góc 60 ° tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng α ?
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là α = 120 ° . Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.
Cho hình nón (N) có đường sinh tạo với đáy một góc
60
0
. Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn ngoại tiếp bằng 2. Thế tích V của khối nón (N).
Đọc tiếp
Cho hình nón (N) có đường sinh tạo với đáy một góc 60 0 . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn ngoại tiếp bằng 2. Thế tích V của khối nón (N).
![]()
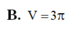
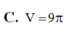
![]()
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng
α
. Gọi I là một điểm trên đường cao DO của hình nón sao cho
DI
DO
k (0 k 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Đọc tiếp
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Gọi I là một điểm trên đường cao DO của hình nón sao cho DI DO = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Một khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng
3
c
m
2
. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc
60
0
chia khối nón thành hai phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm). A. 4,36
c
m
3
B. 5,37
c
m
3...
Đọc tiếp
Một khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng 3 c m 2 . Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 60 0 chia khối nón thành hai phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
A. 4,36 c m 3
B. 5,37 c m 3
C. 5,61 c m 3
D. 4,53 c m 3
Cho hình nón đỉnh S, chiều cao S0h, bán kính đáy bằng R. Gọi M là điểm nằm trên đoạn SO, đặt OMx (
0
x
h
Cắt hình nón bằng mặt phẳng (P) đi qua M và vuông góc với SO, thiết diện thu được là đường tròn (C). Tìm x để thể tích của khối nón đỉnh O đáy là hình tròn giới hạn bởi (C) đạt giá trị lớn nhất.
Đọc tiếp
Cho hình nón đỉnh S, chiều cao S0=h, bán kính đáy bằng R. Gọi M là điểm nằm trên đoạn SO, đặt OM=x ( 0 < x < h Cắt hình nón bằng mặt phẳng (P) đi qua M và vuông góc với SO, thiết diện thu được là đường tròn (C). Tìm x để thể tích của khối nón đỉnh O đáy là hình tròn giới hạn bởi (C) đạt giá trị lớn nhất.
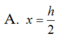
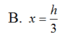
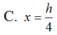
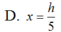
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là
β
. Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng. A.
2
R
3
π
9
tan
β...
Đọc tiếp
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng.
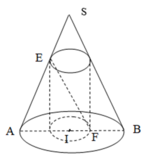
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β




