Phương pháp:
Xác suất của biến cố A được tính bởi công thức: P A = n A n Ω
Cách giải:
Số cách chọn 3 đỉnh bất kì của đa giác là: n Ω = C 48 3
Gọi O là tâm đường tròn ngoại tiếp đa giác đều.
Gọi biến cố A: “Chọn 3 đỉnh bất kì của đa giác để được một tam giác nhọn”.
Lấy điểm A thuộc đường tròn (O), kẻ đường kính AA’ => A’ cũng thuộc đường tròn (O).
Khi đó AA’ chia đường tròn (O) thành hai nửa, mỗi nửa có 23 đỉnh.
Chọn 2 đỉnh B, C cùng thuộc 1 nửa đường tròn có C 23 2 c á c h c h ọ n ⇒ có C 23 2 tam giác ABC là tam giác tù.
Tương tự như vậy đối với nửa còn lại nên ta có 2 C 23 2 tam giác tù được tạo thành.
Đa giác đều có 48 đỉnh nên có 24 đường chéo => có 24.2. C 23 2 tam giác tù.
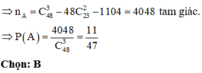
Ứng với mỗi đường kính ta có 23.2 tam giác vuông. Vậy số tam giác vuông là: 23.2.24 = 1104 tam giác.



