Các câu hỏi tương tự
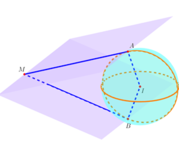
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn
I
M
3
R
2
. Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng: A. ABR B. ABR
3
C. AB
3
R
2
D. ABR hoặc ABR
3
Đọc tiếp
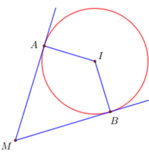
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C. AB= 3 R 2
D. AB=R hoặc AB=R 3
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn
I
M
3
R
2
. Hai mặt phẳng (P), (Q) qua M và tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng
60
o
. Độ dài đoạn thẳng AB bằng: A. ABR B. ABR
3
C
.
A
B
3...
Đọc tiếp
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M và tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60 o . Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C . A B = 3 R 2
D . A B = R h o ặ c A B = R 3
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Qua A kẻ 2 tiếp tuyến từ (S) có tiếp điểm lần lượt là M,N và góc MAN là 60°. Độ dài MN là
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
Cho điểm A nằm trên mặt cầu (S) tâm O, bán kính R6 cm. Gọi I, K lần lượt là hai điểm trên đoạn OA sao cho OIIKKA. Các mặt phẳng (P), (Q) lần lượt đi qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo đường tròn có bán kính
r
1
,
r
2
. Tính tỉ số
r
1
r
2
.
Đọc tiếp
Cho điểm A nằm trên mặt cầu (S) tâm O, bán kính R=6 cm. Gọi I, K lần lượt là hai điểm trên đoạn OA sao cho OI=IK=KA. Các mặt phẳng (P), (Q) lần lượt đi qua I, K cùng vuông góc với OA và cắt mặt cầu (S) theo đường tròn có bán kính r 1 , r 2 . Tính tỉ số r 1 r 2 .
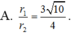
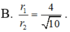
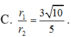
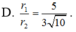
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-20 và mặt phẳng (Q): 2x-y-2z+100 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó A.
r
4
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-2=0 và mặt phẳng (Q): 2x-y-2z+10=0 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
A. r = 4 2 3
B. r = 2 2 3
C. r = 5 3
D. r = 2 5 3
Cho hai đường thẳng
∆
và
∆
′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc
∆
và A’ thuộc
∆
′ . Gọi (P) là mặt phẳng qua A vuông góc với
∆
′ và d là hình chiếu vuông góc của
∆
trên mặt phẳng (P). Đặt AA’ a, góc nhọn giữa
∆
và d là
α
. Mặt phẳng (Q) song song với mặt phẳng (P) cắt ...
Đọc tiếp
Cho hai đường thẳng ∆ và ∆ ′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc ∆ và A’ thuộc ∆ ′ . Gọi (P) là mặt phẳng qua A vuông góc với ∆ ′ và d là hình chiếu vuông góc của ∆ trên mặt phẳng (P). Đặt AA’ = a, góc nhọn giữa ∆ và d là α . Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆ ′ lần lượt tại M và M’. Gọi M 1 là hình chiếu vuông góc của M lên mặt phẳng (P).
Chứng minh 5 điểm A, A’, M, M’, M 1 cùng nằm trên mặt cầu (S). xác định tâm O của (S). Tính bán kính của (S) theo a, α và khoảng cách x giữa hai mặt phẳng (P) và (Q).
Cho hình cầu tâm O bán kính R , tiếp xúc với mặt phẳng (P) . Một hình nón tròn xoay có đáy nằm trên (P), có chiều cao h 15 , có bán kính đáy bằng R . Hình cầu và hình nón nằm về một phía đối với mặt phẳng (P) . Người ta cắt hai hình đó bởi mặt phẳng (Q) song song với (P) và thu được hai thiết diện có tổng diện tích là S . Gọi x là khoảng cách giữa (P) và (Q),
(
0
x
≤
5...
Đọc tiếp
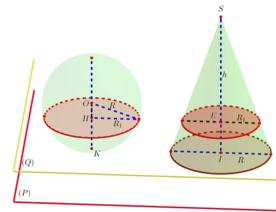
Cho hình cầu tâm O bán kính R , tiếp xúc với mặt phẳng (P) . Một hình nón tròn xoay có đáy nằm trên (P), có chiều cao h = 15 , có bán kính đáy bằng R . Hình cầu và hình nón nằm về một phía đối với mặt phẳng (P) . Người ta cắt hai hình đó bởi mặt phẳng (Q) song song với (P) và thu được hai thiết diện có tổng diện tích là S . Gọi x là khoảng cách giữa (P) và (Q), ( 0 < x ≤ 5 ) . Biết rằng S đạt giá trị lớn nhất khi x = a b (phân số a b tối giản). Tính giá trị T =a+b .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;1), B(3;-1;1), C(-1;-1;1). Gọi
S
1
là mặt cầu tâm A, bán kính bằng 2;
S
2
và
S
3
là hai mặt cầu có tâm lần lượt là B, C và bán kính đều bằng 1. Trong các mặt phẳng tiếp xúc với cả 3 mặt cầu
S
1
,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;1), B(3;-1;1), C(-1;-1;1). Gọi S 1 là mặt cầu tâm A, bán kính bằng 2; S 2 và S 3 là hai mặt cầu có tâm lần lượt là B, C và bán kính đều bằng 1. Trong các mặt phẳng tiếp xúc với cả 3 mặt cầu S 1 , S 2 , S 3 có bao nhiêu mặt phẳng vuông góc với mặt phẳng (Oyz)?
A. 3
B. 1
C. 4
D. 2