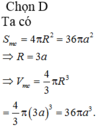Các câu hỏi tương tự
Cho mặt cầu có diện tích bằng
36
πa
2
. Thể tích khối cầu là
Đọc tiếp
Cho mặt cầu có diện tích bằng 36 πa 2 . Thể tích khối cầu là
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có diện tích bằng
4
π
. Thể tích khối cầu (S) bằng
Đọc tiếp
Cho mặt cầu (S) có diện tích bằng 4 π . Thể tích khối cầu (S) bằng
![]()
![]()
![]()
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu. A.
R
3
V
S
B.
R
S
3
V
C.
R
4
V
S
D.
R
V
3
S
Đọc tiếp
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một hình tròn có diện tích
9
π
cm
2
. Tính thể tích khối cầu (S).
Đọc tiếp
Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một hình tròn có diện tích 9 π cm 2 . Tính thể tích khối cầu (S).
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có diện tích
4
πa
2
cm
2
. Khi đó, thể tích khối cầu (S) là
Đọc tiếp
Cho mặt cầu (S) có diện tích
4 πa 2 cm 2 . Khi đó, thể tích khối cầu
(S) là
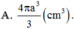
![]()
![]()
![]()
I. Trắc nghiệm ( 6 điểm)Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu. A.
R
3
V
S
B.
R
S
3
V
C.
R
4
V
S
D.
R
V
3...
Đọc tiếp
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Cho mặt cầu (S) có bán kính
3
. Trong tất cả các khối trụ nội tiếp mặt cầu (S) (hai đáy của khối trụ là những thiết diện của hình cầu cắt bởi hai mặt phẳng song song), khối trụ có thể tích lớn nhất bằng bao nhiêu ?
Đọc tiếp
Cho mặt cầu (S) có bán kính 3 . Trong tất cả các khối trụ nội tiếp mặt cầu (S) (hai đáy của khối trụ là những thiết diện của hình cầu cắt bởi hai mặt phẳng song song), khối trụ có thể tích lớn nhất bằng bao nhiêu ?
![]()
![]()
![]()
Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm
![]()
![]()
![]()
![]()