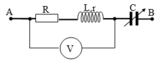
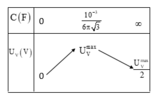
Bài này khảo sát \(U_L\) theo \(C\)
+ Khi C = C1 vôn kế chỉ U1, khi C biến thiên U giảm, do đó C = C1 thì cộng hưởng xảy ra.
\(Z_L=Z_{C1}\)
+ Khi C2=2C1 \(\Rightarrow Z_{C2}=\dfrac{Z_{C1}}{2}=\dfrac{Z_L}{2}\)
\(U_2=\dfrac{U_1}{2}\) \(\Rightarrow I_2=\dfrac{I_1}{2}\) (vì ZL không đổi)
\(\Rightarrow Z_2=2Z_1\)
\(\Rightarrow \sqrt{R^2+(\dfrac{Z_L}{2})^2}=2R\)
\(\Rightarrow Z_L=Z_{C1}=2\sqrt 3 R\)
+ Để U3 = U2/2 = U1/4
\(\Rightarrow I_3=I_1/4\)
\(\Rightarrow Z_3=4Z_1\)
\(\Rightarrow \sqrt{R^2+(Z_L-Z_{C3})^2}=4R\)
\(\Rightarrow |Z_L-Z_{C3}|=\sqrt {15} R\)
\(\Rightarrow |Z_{C1}-Z_{C3}|=\sqrt{15}.\dfrac{2}{\sqrt 3}Z_{C1}=2\sqrt 5 Z_{C1}\)
\(\Rightarrow Z_{C3}=(1+2\sqrt 5)Z_{C1}\)
\(\Rightarrow C_3=\dfrac{C_1}{1+2\sqrt5}\)
chỗ cuối vẫn còn 1 TH âm nữa vì là trị tuyệt đối mà :)