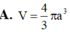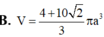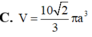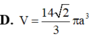Các câu hỏi tương tự
Cho lục giá đều ABCDEF có cạnh bằng 4. Cho lục giác đều đó quanh quay đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra. A.
V
128
π
B.
V
32
π
C.
V
16
π
D.
V
64
π
Đọc tiếp
Cho lục giá đều ABCDEF có cạnh bằng 4. Cho lục giác đều đó quanh quay đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra.
A. V = 128 π
B. V = 32 π
C. V = 16 π
D. V = 64 π
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB A.
3
π
4
B.
π
4
C.
π
8
D.
π
3
2
Đọc tiếp
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB
A. 3 π 4
B. π 4
C. π 8
D. π 3 2
Cho tam giác ABC có Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có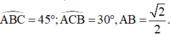 
Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
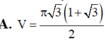
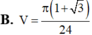
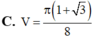
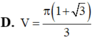
Cho hình lăng trụ có tất cả các cạnh đều bằng a, đáy là hình lục giác đều, góc tạo nên bởi cạnh bên và đáy bằng
60
0
. Tính thể tích V khối lăng trụ. A.
V
3
4
a
3
B.
V
3
4
a
3
C. ...
Đọc tiếp
Cho hình lăng trụ có tất cả các cạnh đều bằng a, đáy là hình lục giác đều, góc tạo nên bởi cạnh bên và đáy bằng 60 0 . Tính thể tích V khối lăng trụ.
A. V = 3 4 a 3
B. V = 3 4 a 3
C. V = 9 4 a 3
D. V = 3 3 2 a 3
Trong không gian, cho hình chữ nhật ABCD có AB 2, AD 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d. A. V 17
π
B. V 5
π
C. V 15
π
D. 30
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. 30 π
Cho tứ diện ABCD có AD
⊥
(ABC), ABC là tam giác vuông tại B. Biết BCA, ABa
3
, AD3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
Đọc tiếp
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
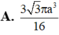
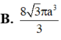
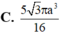
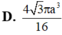
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8
π
Tính chiều cao của hình nón này.
Đọc tiếp
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
Cho một lục giác đều ABCDEF. Viết các chữ cái A, B, C, D, E, F vào sáu cái thẻ. Lấy ngẫu nhiên hai thẻ. Tìm xác suất sao cho đoạn thẳng mà các đầu mút là các điểm được ghi trên hai thẻ đó là:
a. Cạnh của lục giác.
b. Đường chéo của lục giác.
c. Đường chéo nối hai đỉnh đối diện của lục giác.
Cho hình thang cân ABCD có các cạnh đáy và cạnh bên ADBC2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
Đọc tiếp
Cho hình thang cân ABCD có các cạnh đáy 
và cạnh bên AD=BC=2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
