Phương pháp:
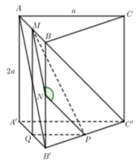
- Gọi M, N, P lần lượt là trung điểm của A B ' , B B ' , B ' C '
- Sử dụng tính chất góc giữa hai đường chéo nhau bằng góc giữa hai đường thẳng cùng thuộc 1 mặt phẳng mà lần lượt song song với hai đường thẳng đã cho.
Cách giải:

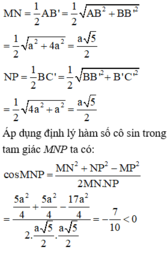

Phương pháp:
- Gọi M, N, P lần lượt là trung điểm của A B ' , B B ' , B ' C '
- Sử dụng tính chất góc giữa hai đường chéo nhau bằng góc giữa hai đường thẳng cùng thuộc 1 mặt phẳng mà lần lượt song song với hai đường thẳng đã cho.
Cách giải:


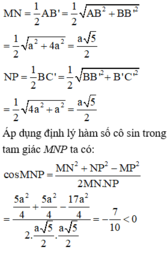

Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, AB = AC = a, BAC = 120 ° BB' = a, I là trung điểm CC'. Gọi α là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
A. c o s α = 3 10
B. c o s α = 3 10
C. c o s α = 3 10
D. c o s α = 3 5
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B, AB = a, BC = 2a. Biết thể tích của khối lăng trụ ABC.A’B’C’ bằng 2 2 a 3 . Gọi α là góc giữa mặt phẳng (A’BC) với mặt phẳng (ABC). Khi đó cos của góc α bằng:
![]()
![]()
![]()
![]()
Cho khối lăng trụ tam giác có đáy là tam giác A B C . A 1 B 1 C 1 đều cạnh 2a, điểm A 1 cách đều ba điểm A, B, C . Cạnh bên A A 1 tạo với mặt phẳng đáy một góc α . Thể tích khối trụ A B C . A 1 B 1 C 1 bằng 2 3 a 3 . Giá trị của α là.
A. 30 0
B. 45 0
C. 45 0
D. Đáp án khác
Cho hình lăng trụ đều ABC.A’B’C’. Biết khoảng cách từ điểm C đến mặt phẳng (ABC’) bằng a, góc giữa 2 mặt phẳng (ABC’) và (BCC’B’) bằng a với cos α = 1 3 (tham khảo hình vẽ dưới đây). Thể tích khối lăng trụ ABC.A’B’C’ bằng

A. 3 a 2 15 10
B. 3 a 3 15 20
C. 9 a 3 15 10
D. 9 a 3 15 20
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho góc α thỏa mãn cos α = 3 5 và - π < α < 0 A = sin 2 α - cos 2 α . Tính giá trị biểu thức . A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là
A. 3 a 2 bsinα 12
B. 3 a 2 bcosα 12
C. 3 a 2 bcosα 4
D. 3 a 2 bsinα 4
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là
A. 3 a 2 b sin α 12
B. 3 a 2 b cos α 4
C. 3 a 2 b sin α 4
D. 3 a 2 b cos α 12
Cho góc α thỏa mãn 5 sin 2 α - 6 cos α = 0 và 0 < α < π 2 .
Tính giá trị của biểu thức: A = cos ( π 2 - α ) + sin ( 2015 π - α ) - c o t ( 2016 π + α ) .
A. - 2 15
B. 4 15
C. 1 15
D. - 3 5