Dùng phép tịnh tiến vectơ AE → biến lăng trụ ABC.EFG thành lăng trụ EFG.A’B’C .
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số
V
1
V
2
có giá trị là A.
1
4
B.
1
2
C.
1
3...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 1 3
D. 3 4
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số
V
1
V
2
có giá trị là A.
1
4
B.
1
2
C. 3 D.
1...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 3
D. 1 3
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Cho hình lăng trụ ABC.ABC. Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích
V
1
và
V
2
như hình vẽ. Tỉ số
V
1
V
2
là A.
1
2
B. 1 C.
1...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tỉ số V 1 V 2 là
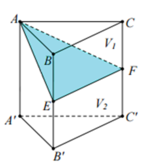
A. 1 2
B. 1
C. 1 3
D. 1 4
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho AM2MA, NB2NB, PCPC. Gọi
V
1
,
V
2
lần lượt là thể tích của hai khối đa diện ABCMNP và A’B’C’MNP. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho AM=2MA', NB'=2NB, PC=PC'. Gọi V 1 , V 2 lần lượt là thể tích của hai khối đa diện ABCMNP và A’B’C’MNP. Tính tỉ số V 1 V 2
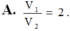
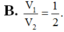
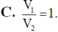
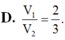
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho
A
M
+
B
N
+
C
P
1
. Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto
u
→
I
A
→
+
I
B...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ = 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho A M + B N + C P = 1 . Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto u → = I A → + I B → + I C → bằng
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.A’B’C’ có
A
B
1
,
A
C
2
,
A
A
3
và
B
A
C
⏜
120
0
. Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM3BM; CN2CN. Tính khoảng cách từ điểm M đến mặt phẳng (ABN).
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có A B = 1 , A C = 2 , A A ' = 3 và B A C ⏜ = 120 0 . Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM=3B'M; CN=2C'N. Tính khoảng cách từ điểm M đến mặt phẳng (A'BN).
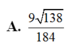
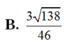
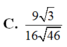

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần,
V
1
là thể tích của phần đa diện chứa điểm B,
V
2
là phần đa diện còn lại. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 là phần đa diện còn lại. Tính tỉ số V 1 V 2
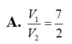
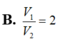
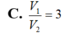
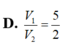
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần,
V
1
là thể tích của phần đa diện chứa điểm B,
V
2
thể tích phần đa diện còn lại. Tính tỉ số
V
1
V
2
A.
V
1...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2



