Đáp án A
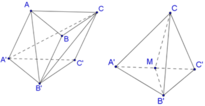
Dễ dàng tính được các cạnh của tứ diện CA’B’C’:


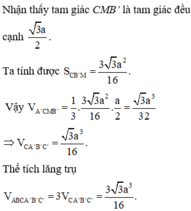
Đáp án A

Dễ dàng tính được các cạnh của tứ diện CA’B’C’:


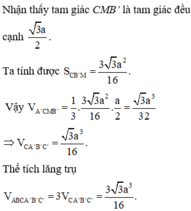
Cho hình lăng trụ tam giác đều ABCA’B’C’ có cạnh đáy bằng a, khoảng cách từ tâm O của tam giác đều ABC đến mặt phẳng (A'BC) bằng a/6. Tính thể tích V của khối lăng trụ ABCA’B’C’
A. V = a 3 3 3 16
B. V = a 3 2 6
C. V = a 3 3 2 16
D. V = a 3 3 6
Lăng trị ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A' lên (ABC) trùng với tâm O của tam giác ABC. Mặt phẳng (P) chứa BC vuông góc với AA' cắt lăng trụ theo thiết diện có diện tích bằng a 2 3 8 . Thể tích khối lăng trụ ABCA’B’C' bằng.
A. a 3 2 12
B. a 3 6 12
C. a 3 6 3
D. a 3 3 12
Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi, A ' AC ^ = 60 o , B ' C = a 3 2 . Tính thể tích lăng trụ ABCA′B′C′.
A. 3 a 3 4
B. 3 3 a 3 4
C. 3 3 a 3 16
D. 3 a 3 16
Cho một khối lăng trụ có thể tích là 3 .a 3 , đáy là tam giác đều cạnh a. Tính chiều cao h của khối lăng trụ.
A. h = 4a
B. h = 3a
C. h = 2a
D. 12a
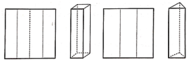
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi V 1 ; V 2 lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh V 1 và V 2
A. V 1 > V 2
B. V 1 = V 2
C. V 1 < V 2
D. Không so sánh được
Cho hình lăng trụ ABCA’B’C’ có đáy tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB, góc giữa A’C và mặt đáy bằng 60 ° . Tính khoảng cách h giữa hai đường thẳng AC và BB
A. h = 6 a 52
B. h = 3 a 52
C. a 3 4
D. 4 a 3
Cho hình lăng trụ ABCA’B’C’ có đáy tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB, góc giữa A’C và mặt đáy bằng 60 ° . Tính khoảng cách h giữa hai đường thẳng AC và BB.
A. h = 6 a 52
B. h = 3 a 52
C. h = a 3 4
D. 4a 3
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy a=3. Biết tam giác A’BA có diện tích bằng 6. Thể tích tứ diện ABB’C’ bằng:
A. 3 3
B. 3 3 2
C. 6 3
D. 9 3
Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:
- Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là V 1 (Hình 1).
- Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là V 2 (Hình 2).
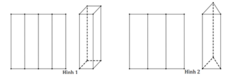
Tính tỉ số k = V 1 V 2
A. k = 3 3 8
B. k = 3 3 2
C. k = 4 3 9
D. k = 3 3 4