Các câu hỏi tương tự
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Cho khối lăng trụ đứng
A
B
C
.
A
,
B
,
C
,
có
B
B
,
a
, đáy ABC là tam giác vuông cân tại B và
A
C
a
2
. Tính thể tích V của khối lăng trụ đã cho. A.
V
a
3...
Đọc tiếp
Cho khối lăng trụ đứng A B C . A , B , C , có B B , = a , đáy ABC là tam giác vuông cân tại B và A C = a 2 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 .
B. V = a 3 3 .
C. V = a 3 6 .
D. V = a 3 2 .
Cho hình lăng trụ đứng ABC.A B C có đáy ABC là tam giác vuông tại A, biết AB a, AC 2a và A B 3a. Tính thể tích của khối lăng trụ ABC.A B C.
Đọc tiếp
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
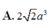
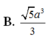
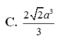
![]()
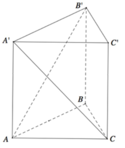
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.
Đọc tiếp
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB = 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.
![]()
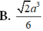
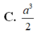
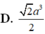
cho hình lăng trụ đứng ABCA'B'C' có đáy tam giác ABC vuông tại B. AB=1. A'B tạo với đáy 1 góc 60°. Tính VABCA'B'C'
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C A.
π
2
a
3
3
B.
8
π
2
a
3...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hình chiếu của C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính theo a thể tích khối cầu đi qua năm điểm A, B, B’, A’ và C
A. π 2 a 3 3
B. 8 π 2 a 3 81
C. π 2 a 3 24
D. π 2 a 3 81
Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A’B’C’ có
A
3
;
-
1
;
1
, hai đỉnh B, C thuộc trục Oz và AA’1 (C không trùng với O). Biết véctơ
u
→
a
;
b
;
2
với...
Đọc tiếp
Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A’B’C’ có A ' 3 ; - 1 ; 1 , hai đỉnh B, C thuộc trục Oz và AA’=1 (C không trùng với O). Biết véctơ u → = a ; b ; 2 với a , b ∈ ℝ là một véctơ chỉ phương của đường thẳng A’C. Tính T = a 2 + b 2
A. 5
B. 16
C. 4
D. 9
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho hình lăng trụ đứng
A
B
C
.
A
,
B
,
C
,
đáy là tam giác vuông cân tại
B
,
A
C
2
biết góc giữa
(
A
,
B
C
)
và
(
A
B
C
)
bằng
60...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A , B , C , đáy là tam giác vuông cân tại B , A C = 2 biết góc giữa ( A , B C ) và ( A B C ) bằng 60 0 . Thể tích của khối lăng trụ bằng:
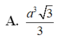
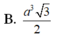
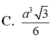
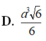
Cho khối lăng trụ đứng ABC.A’B’C’ có BBa, đáy ABC là tam giác vuông cân tại B và ACa
2
.
Tính thể tích V của khối lăng trụ đã cho
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có BB'=a, đáy ABC là tam giác vuông cân tại B và AC=a 2 . Tính thể tích V của khối lăng trụ đã cho
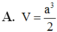
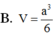
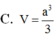
![]()