Đáp án D
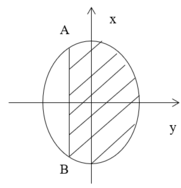
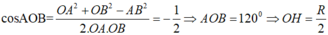
Chọn hệ trục tọa độ như hình vẽ ⇒ pt đường tròn đáy là:
![]()
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
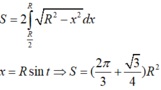
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
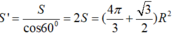
Đáp án D

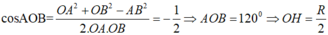
Chọn hệ trục tọa độ như hình vẽ ⇒ pt đường tròn đáy là:
![]()
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
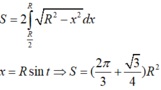
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
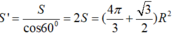
Cho hình trụ có hai đáy là hai hình tròn (O) và (O'), chiều cao bằng 2R và bán kính đáy R. mặt phẳng (P) đi qua trung điểm của (OO') và tạo với OO' một góc 30 o cắt đường tròn dáy theo dây cung . Tính độ dài day cung đó theo R
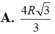
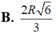
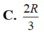
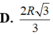
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
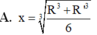
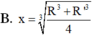
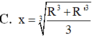
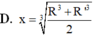
Cho một hình trụ có hai đáy là hai đường tròn(O ; R) với OO' = R 3 và một hình nón có đỉnh O’ và đáy là hình tròn(O; R) Ký hiệu S 1 ; S 2 lần lượt là diện tích xung quanh của hình trụ và hình nón. Tính k = S 1 S 2
A. k = 1 3
B. k = 2
C. k = 3
D. k = 1 2
Hình trụ có bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy, với OO’ = 2r .Một mặt cầu (S ) tiếp xúc với hai đáy hình trụ tại O và O'. Gọi VC và VT lần lượt là thể tích khối cầu và khối trụ tương ứng. Khi đó V C V T bằng:
A. 1 2
B. 3 4
C. 2 3
D. 3 5
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính R và chiều cao là R 2 . Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho góc của hai đường thẳng OA và OB bằng α không đổi. Tính AB theo R và α .
A . R 1 + 4 sin 2 α 2
B . R + 4 sin 2 α 2
C . R 2 + 4 sin 2 α
D . R 1 + 4 sin 2 α
Cho hình nón đỉnh S, đáy là đường tròn (O;r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8 r 5 . Tính theo r khoảng cách từ O đến (SAB)
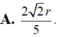
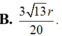
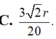
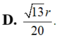
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây là đúng ? Tính bán kính mặt cầu ngoại tiếp hình chóp theo a.
A. tan α = 2
B. tan α = 1 2
C. tan α = 1 2
D. tan α = 1
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
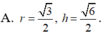


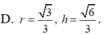
Một hình trụ có diện tích xung quanh bằng 4 π thiết diện qua trục là hình vuông. Một mặt phẳng ( α ) song song với trục, cắt hình trụ theo thiết diện là tứ giác ABB’A’, biết một cạnh của thiết diện là một dây cung của đường tròn đáy của hình trụ và căng một cung 120 o Tính diện tích thiết diện ABB’A’?
A. 3 2
B. 3
C. 2 3
D. 2 2