Các câu hỏi tương tự
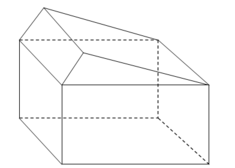
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A B C là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA2/3. Mặt phẳng (SA B ) chia khối đa diện đã cho thành hai phần. Gọi
V
1
là thể tích phần khối đa diện chứa đỉnh A,
V
2
là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng A.
72
V
1...
Đọc tiếp
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
45
°
. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích
V
1
khối đa diện còn lại có thể tích
V
2
(tham khảo hình vẽ bên đây). T...
Đọc tiếp
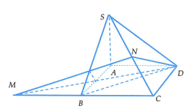
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho các khối đa diện đều như hình vẽ sau đây. Khối đa diện đều loại {3;5} là hình nào?
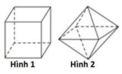
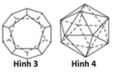
A. Hình 4
B. Hình 1
C. Hình 2
D. Hình 3
Cho hình lăng trụ ABC.A’B’C’, M là trung điểm của CC’. Mặt phẳng (ABM) chia khối lăng trụ thành hai khối đa diện. Gọi
V
1
là thể tích khối đa diện chứa đỉnh C và
V
2
là thể tích khối đa diện còn lại. Tính tỉ số
V
1
V
2
A.
2
5
B.
1...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’, M là trung điểm của CC’. Mặt phẳng (ABM) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích khối đa diện chứa đỉnh C và V 2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2
A. 2 5
B. 1 6
C. 1 2
D. 1 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh
a
,
B
A
D
⏜
60
0
và SA vuông góc với mặt phẳng
A
B
C
D
. Góc giữa hai mặt ph...
Đọc tiếp
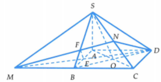
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , B A D ⏜ = 60 0 và SA vuông góc với mặt phẳng A B C D . Góc giữa hai mặt phẳng S B D và A B C D bằng 45 0 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng M N D chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 và khối đa diện còn lại có thể tích bằng V 2 . Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Gọi M, N lần lượt là trung điểm của cạnh
A
B
và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và
H
là khối đa diện còn lại. Tính tỉ số
V...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi M, N lần lượt là trung điểm của cạnh A ' B ' và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và H ' là khối đa diện còn lại. Tính tỉ số V H V H '
A. V H V H ' = 55 89
B. V H V H ' = 37 48
C. V H V H ' = 1 2
D. V H V H ' = 2 3
Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối đa diện đó, lúc đó ta có A. C là số chia hết cho 3 B. C là số chẵn. C. C là số lẻ. D. C là số chia hết cho 5.
Đọc tiếp
Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối đa diện đó, lúc đó ta có
A. C là số chia hết cho 3
B. C là số chẵn.
C. C là số lẻ.
D. C là số chia hết cho 5.
Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh?
A. 20.
B. 18.
C. 15.
D. 12.