Gọi O là giao điểm của AC và BD.
Mặt phẳng (SAC) và (SBD) chia khối chóp S.ABCD thành mấy khối chóp thành 4 khối chóp là các khối chóp sau S.ABO, S.ADO, S.CDO, S.BCO.
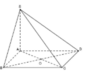
Đáp án cần chọn là A
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Gọi O là giao điểm của AC và BD.
Mặt phẳng (SAC) và (SBD) chia khối chóp S.ABCD thành mấy khối chóp thành 4 khối chóp là các khối chóp sau S.ABO, S.ADO, S.CDO, S.BCO.

Đáp án cần chọn là A
Cho khối chớp S.ABCD, hỏi hai mặt phẳng (SAC) và (SBD) chia khối chóp S.ABCD thành mấy khối chóp ?
A. 4
B. 3
C. 5
D. 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, AB = a , AD = 2 a . . Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 . Thể tích khối chóp S.ABCD bằng
A. 2 3 a 3 3
B. 3 a 3 6
C. 3 a 3 3
D. 3 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng S A C và S B D cùng vuông góc với đáy, A B = a , A D = 2 a . Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 . Thể tích khối chóp S.ABCD bằng
A. 2 3 a 3 3
B. 3 a 3 3
C. 3 a 3 2
D. 3 a 3 6
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, A C = 2 a 3 , B D = 2 a . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD). Biết khoảng cách từ tâm O đến (SAB) bằng a 3 4 tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 2 3
B. V = a 3 3 3
C. V = a 3 3 9
D. V = a 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, A C = 2 3 a , B D = 2 a , hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến (SAB) bằng a 3 4 . Thể tích của khối chóp S.ABCD là:
A. a 3 3 12
B. a 3 3 3
C. a 3 3 18
D. a 3 3 16
Cho khối chóp tử giác S.ABCD. Mặt phẳng đi qua trọng tâm các tam giác SAB, SAC, SAD chia khối chóp này thành hai phần có thể tích là V 1 và V 2 ( V 1 < V 2 ) . Tính tỉ lệ V 1 V 2 .
A. 8 27
B. 16 81
C. 8 19
D. 16 75
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , B A D ⏜ = 60 0 và SA vuông góc với mặt phẳng A B C D . Góc giữa hai mặt phẳng S B D và A B C D bằng 45 0 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng M N D chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 và khối đa diện còn lại có thể tích bằng V 2 . Tính tỉ số V 1 V 2
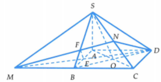
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
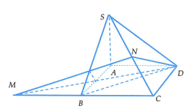
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5