\(AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{3a}{\sqrt{2}}\)
\(\Rightarrow V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a.\dfrac{1}{2}.\left(\dfrac{3a}{\sqrt{2}}\right)^2=\dfrac{3a^3}{2}\)
Cho khối chóp S. ABC , có mặt bên SAB là tam giác vuông cân tại S có SA = 3 cm và mặt bên SAB vuông góc với mặt đáy ABC . Mặt đáy là ΔABC vuông cân tại A. Tính khối chóp S. ABC.
Cho khối chóp S . ABC có đáy là tam giác ABC cân tại A, BAC = 120o, AB = a. Cạnh bên SA vuông góc với mặt đáy, SA = a. Thể tích khối chóp đã cho bằng
A. a 3 3 4
B. a 3 3 12
C. a 3 3 2
D. a 3 3 6
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, SA=3a và SA vuông góc với mặt phẳng đáy, SB tạo với mặt phẳng đáy một góc 60 o . Tính thể tích khối chóp S.ABC.
A. 3 a 3
B. 27 a 3
C. 9 a 3
D. 3 a 3 2
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA=a tam giác ABC là tam giác vuông cân tại A, AB=2a. Tính theo a thể tích V của khối chóp S.ABC
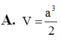
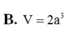
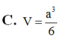
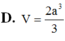
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy A B C . Biết S A = a tam giác ABC là tam giác vuông cân tại A, A B = 2 a . Tính theo a thể tích V của khối chóp S.ABC.
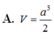
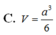
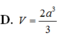
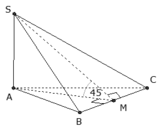
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a 2 , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng
A. a 3 2 6
B. a 3 2 2
C. a 3 2 4
D. a 3 2 12
Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết V S . A E F = 1 4 V S . A B C . Tính thể tích V của khối chóp S. ABC.
A. a 3 2
B. a 3 8
C. 2 a 3 5
D. a 3 12
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC = 3 a , SA = 2 a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
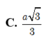
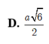
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
