Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và ACa) Chứng minh rằng ΔAEF ΔACBb) Cho AH 4,8cm, BC 10 cm. Tính SAEF?c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC
a) Chứng minh rằng ΔAEF ![]() ΔACB
ΔACB
b) Cho AH = 4,8cm, BC = 10 cm. Tính SAEF?
c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Cho hình chữ nhật ABCD có AB=8cm , BC=6cm . gọi H là chân đường vuông góc kẻ từ A xuống BD , phân giác của góc BCD cắt BD ở E
a) chứng minh tam giác AHB đồng dạng với tam giác BCD
b) chứng minh AH.ED=HB.EB
c) Tính diện tích tứ giác AECH
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm. Kẻ đường trung tuyến AM (MÎBC). Qua M kẻ đường thẳng vuông góc với BC cắt AC tại D.
a) Chứng minh
b) Tính độ dài đoạn thẳng BC và DM.
c) Gọi E là chân đường vuông góc kẻ từ C đến đường thẳng BD. Chứng minh rằng:
CD.CA + BD.BE = BC2
Mọi người giúp em với ạ cần gấp
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho hình thoi ABCD có widehat{ABC} 90^0. Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho widehat{MON}widehat{DAC}. Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!Em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho hình thoi ABCD có \(\widehat{ABC}< 90^0\). Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho \(\widehat{MON}=\widehat{DAC}\). Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Cho Delta ABC có H là trực tâm . Gọi P là 1 điểm thuộc đoạn thẳng AB , gọi Q là 1 điểm thuộc đoạn thẳng AC sao cho widehat{BHP}widehat{CHQ}90^0 . Gọi M là trung điểm của đoạn thẳng BC. Chứng minh rằng HM vuông góc với PQ .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn ạ!
Đọc tiếp
Cho \(\Delta ABC\) có H là trực tâm . Gọi P là 1 điểm thuộc đoạn thẳng AB , gọi Q là 1 điểm thuộc đoạn thẳng AC sao cho \(\widehat{BHP}=\widehat{CHQ}=90^0\) . Gọi M là trung điểm của đoạn thẳng BC. Chứng minh rằng HM vuông góc với PQ .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn ạ!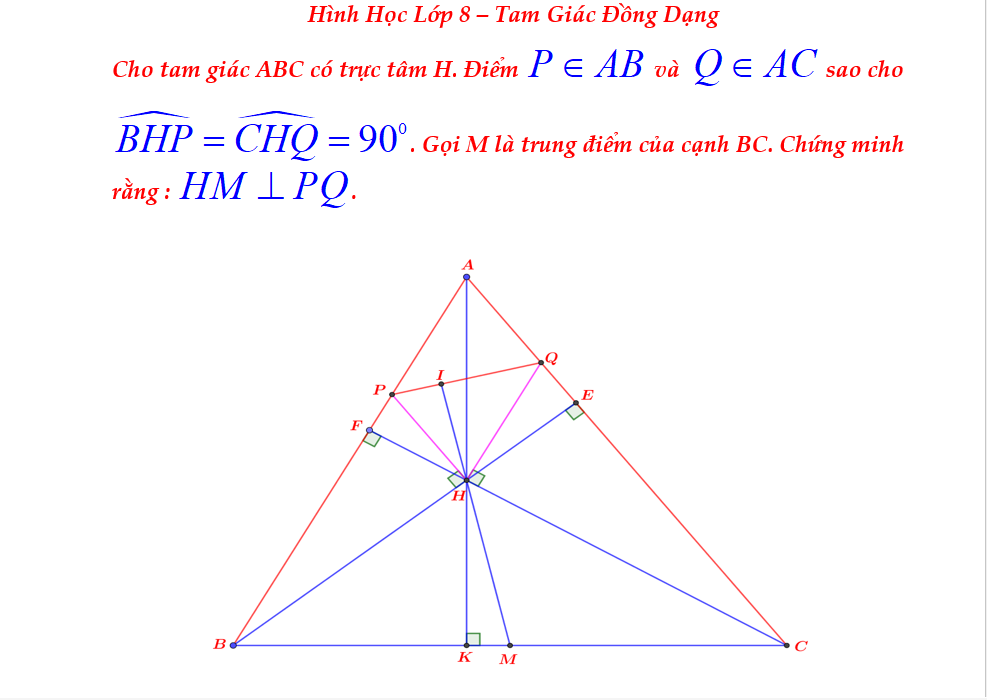
Cho hình bình hành ABCD (góc A nhỏ hớn 90 độ), lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
cho tam giác abc vuông tại a gọi m là trung điểm của ac kẻ md vuông góc ab tại d
a) chứng minh adme là hình chữ nhật
b) kẻ ah vuông góc bc tại h chứng minh góc bah = góc ach
Cho hình vuông ABCD có AB = a, hai đường chéo cắt nhau tại O. Trên hai cạnh AB, BC lần lượt lấy hai điểm E và G sao cho AE= BG. Gọi H là giao điểm của tia AG và tia DC, I là giao điểm của tia OG và đoạn thẳng BH.
1) Chứng minh rằng: AOGE là tam giác vuông cân.









