Question

Cho hình vẽ sau, biết OA = OB; góc OAC = góc OBD.

a) Chứng minh rằng AC = BD; OC = OD; AD = BC.

b) Chứng minh rằng tam giác ADC = tam giác BCD.
c) Gọi I là giao điểm của AC và BD. Chứng minh rằng IA = IB và IC = ID.

d) Chứng minh rằng OI là tia phân giác của góc AOB và OI vuông góc CD.

Answer 1

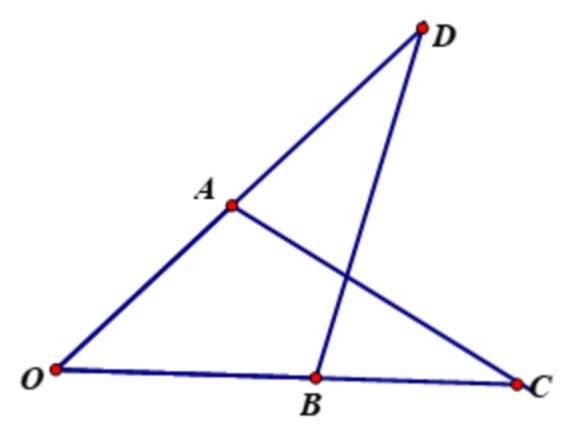
a: Xét ΔOBD và ΔOAC có

\(\widehat{OBD}=\widehat{OAC}\)

OB=OA

\(\widehat{BOD}\) chung

Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC

OB+BC=OC

OA+AD=OD

mà OB=OA và OC=OD

nên BC=AD

b: Xét ΔADC và ΔBCD có

AD=BC

CD chung

AC=BD

Do đó: ΔADC=ΔBCD

c: ΔADC=ΔBCD

=>\(\widehat{IDC}=\widehat{ICD}\)

=>ΔIDC cân tại I

=>ID=IC

ID+IB=BD

IC+IA=AC

mà ID=IC và BD=AC

nên IB=IA

d: Xét ΔOAI và ΔOBI có

OA=OB

AI=BI

OI chung

Do đó: ΔOAI=ΔOBI

=>\(\widehat{AOI}=\widehat{BOI}\)

=>OI là phân giác của góc AOB

=>OI là phân giác của góc COD

ΔCOD cân tại O

mà OI là đường phân giác

nên OI\(\perp\)CD

Answer 2

a, xét tam giác OBD và tam giác OAC có:

góc O chung

OA=OB(gt)

góc OAC= góc OBD(gt)

=>tam giác OBD= tam giác OAC (g.c.g)

=>\(\left\{{}\begin{matrix}AC=BD\\OC=OD\end{matrix}\right.\)(2 cạnh tương ứng)

 

Answer 3

b, Nối D với C

Xét tam giác ADC và tam giác BCD có:

AD=BC ( cmt)

BD=AC(cmt)

CD cạnh chung

=>tam giác ADC =tam giác BCD (c.c.c)