Xét ΔABE có AB=AE
nên ΔABE cân tại A
=>\(\widehat{ABC}=\widehat{AED}\)
Xét ΔABC và ΔAED có
AB=AE
\(\widehat{ABC}=\widehat{AED}\)
BC=DE
Do đó: ΔABC=ΔAED
=>AC=AD
=>ΔACD cân tại A
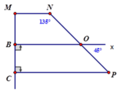
Cho hình vẽ dưới đây. Chứng minh rằng MN // CP và M N ⊥ B C
Cho tam giác ABC cân tại A. Vẽ tia phân giác của góc A cắt BC tại H.
a/ Chứng minh tam giác ABH = tam giác ACH
b/ Trên tia đối của tia AB lấy điểm D sao cho AB=AD. Chứng minh: tam giác ACD cân.
c/ Chứng minh: AH // CD
Cho tam giác ABC cân tại A. Vẽ tia phân giác của góc A cắt BC tại H.
a) Chứng minh: ∆ABH = ∆ACH
b) Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Chứng minh: ∆ACD cân.
c) Chứng minh: AH // CD
d) Tính số đo góc DCB?
Cho hình vẽ dưới đây
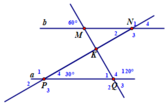a. Chứng minh rằng a // b
b. Tính số đo N 1 ^ ; N 2 ^ ; N 3 ^ ; N 4 ^
Cho hình vẽ biết : CM//AB. Chứng minh CM là tia phân giác của góc ACD
Cho hình vẽ dưới đây.
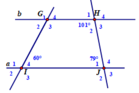a. Chứng minh rằng a // b
b. Tính số đo góc G 1 ^ , G 2 ^ , G 3 ^ , G 4 ^
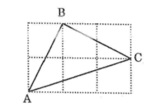
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới) là tam giác vuông cân
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD. Chứng minh rằng ∠(EAF) = 900.
Cho tam giác ABC cân tại A có M là trung điểm của AC . trên tia đối MB lấy điểm D sao cho DM = BM
a, Chứng minh AD song song với BC
b, Tam giác ACD cân
c, Trên tia đối của tia AD lấy điểm E sao cho CH = CE .chứng minh I là trung điểm của BC và DE
nói cách làm và vẽ hình nữa nha
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ), có AD là đường phân giác. chứng minh tam giác ABD = tam giác ACD. Từ C vẽ đường thẳng vuông góc với BC tại C, đường này cắ tia BA tại E. chứng minh tam giác AEC là tam giác cân. Từ A vẽ AM vuông góc EC ( M thuộc EC). Đoạn thẳng ED cắt đoạn thẳng AC tại N. chứng minh ba điểm B,M,N thẳng hàng
