Question

 Cho hình vẽ, biết góc BAC=80 độ, góc ABC = 50 độ, góc xOA =50 độ. At là tia phân giác của góc OAC :

a) Giải thích tại sao Ox song song BC, At song song BC ?

b) Tính góc ACB 

Nhanh lên mình cần gấp!!!!!

Answer 1

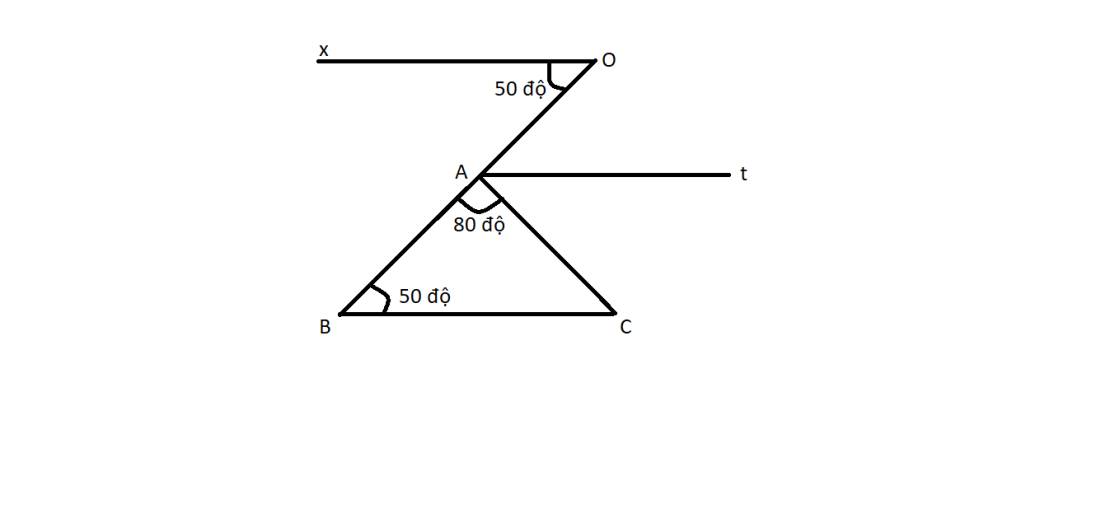
a: 

Xét ΔABC có góc OAC là góc ngoài tại đỉnh A

nên \(\widehat{OAC}+\widehat{BAC}=180^0\)

=>\(\widehat{OAC}=180^0-80^0=100^0\)

At là phân giác của góc OAC

=>\(\widehat{tAO}=\widehat{tAC}=\dfrac{\widehat{OAC}}{2}=\dfrac{100^0}{2}=50^0\)

\(\widehat{tAO}=\widehat{CBA}\)(=50 độ)

mà hai góc này là hai góc ở vị trí đồng vị

nên At//BC

\(\widehat{xOA}=\widehat{ABC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên Ox//BC

 

b: 

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

=>\(\widehat{ACB}+80^0+50^0=180^0\)

=>\(\widehat{ACB}=50^0\)