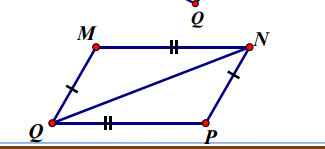
a) Xét \(\Delta MNQvà\Delta PQN\) ta có:
\(\left\{{}\begin{matrix}MN=PQ\\MQ=NP\\NQ:cạnhchung\end{matrix}\right.\)
\(\Rightarrow\Delta MNQ=\Delta PQN\)
Cho hình vẽ bên, trong đó MP song song với NQ. Trên nửa mặt phẳng không chứa điểm P có bờ là đường thẳng MN, vẽ
điểm E sao cho E M N ^ = M N Q ^ . Chứng minh các điểm E, M, P thẳng hàng.
Cho tam giác MNQ. I là trung điểm của MN. K là trung điểm của MQ. Vẽ điểm F sao cho K là trung điểm của IF. a, Chứng minh IN = QF. b, Chứng minh tam giác NIQ = tam giác FQI. c, Chứng minh IK song song với NQ và IQ= 1/2 NQ
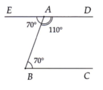
Cho hình vẽ biết:góc MNP=60 độ ; MPN=30 độ:MP vuông góc với PQ
Chứng minh MN song song với PQ
Cho MNP có MN = MP. D là trung điểm của NP. Trên tia đối của tia DM lấy điểm Q sao cho DQ = DM
a) Chứng minh MN = PQ
b) Chứng minh MN//PQ
c) Qua M kẻ đường thẳng song song với NP cắt QP tại E. Chứng minh P là trung điểm của QE
Cho góc xOy nhọn . Từ điểm M trên cạnh Ox dựng MN vuông góc với Oy tại N , dựng NP vuông góc với Ox tại P dựng PQ vuông góc với Oy tại Q , dựng QR vuông góc với Ox tại R . Hãy chứng minh :
a) MN song song với PQ ; NP song song với QR
b) Tìm tất cả các góc bằng góc PNM
Cho tứ giác MNPQ , biết MN song Với QP , MQ song song với NP
cm:
a)MN=PQ
b) MQ=NP (lưu ý chỉ sử dụng hai tam giác băng nhau)
cho tam giác ABC kẻ tia phân giác Bx của góc B , Bx cắt AC tại M. từ M kẻ đường thẳng song song với AB , nó cắt BC tại N . từ N kẻ Ny SONG SONG VỚI Bx chứng minh; a) góc xBC = góc BMN .
b) Ny là tia phân giác của góc MNC . c) gọi P là giao điểm của Ny và AC . trên tia đối của tia MB lấy điểm Q sao cho MQ=NP . chứng minh tam giác MNP = tam giác PQM , MN // PQ
Bài 7: Cho hình vẽ bên Biết MN//PQ, MN = PQ. Chứng minh MQ = NP và MQ //NP.
Cho hình vẽ bên với Ay song song với BC, BC song song với Dz và Bx song song với CD. Chứng minh rằng góc xAy bằng góc CDz.
