Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
![]()
Do đó
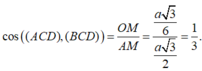
Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
![]()
Do đó
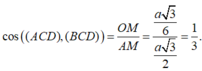
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
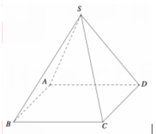
A. 3 3
B. 1 2
C. 3 2
D. 3 6
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của ∆ABC và ∆ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BMN) là:
A. a 2 3 4
B. a 2 11 6
C. a 2 11 8
D. a 2 11 16
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = a r c sin 33 + 1 8
B. φ = a r c sin 33 - 1 8
C. φ = a r c sin 29 + 1 8
D. φ = a r c sin 29 - 1 8
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
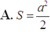


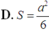
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G 1 G 2 G 3 G 4 .
A. V = 2 4
B. V = 2 18
C. V = 2 32
D. V = 2 12
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
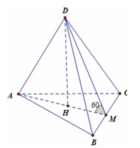
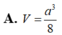
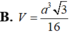
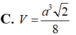
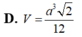
Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng 2a. Cosin của góc tạo bởi cạnh bên và mặt phẳng đáy bằng:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Côsin góc giữa hai mặt phẳng (SAB) và (SAD) bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1, AD= 2 Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau:
1 O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
2 O.ABC là hình chóp tam giác đều.
Hãy chọn khẳng định đúng
A. Chỉ (2) đúng
B. Cả (1) và (2) đều sai.
C. Cả (1) và (2) đều đúng
D. Chỉ (1) đúng