Các câu hỏi tương tự
Cho hình thang cân ABCD (AB//CD) có AB < CD. Gọi O là giao điểm của AD và BC, E là giao điểm của AC và BD. C/m
a) Tam giác AOB cân
b) Tam giác ABD = tgiac BAC
c) EC = ED
d) OE là đường trung trực của AB và CD
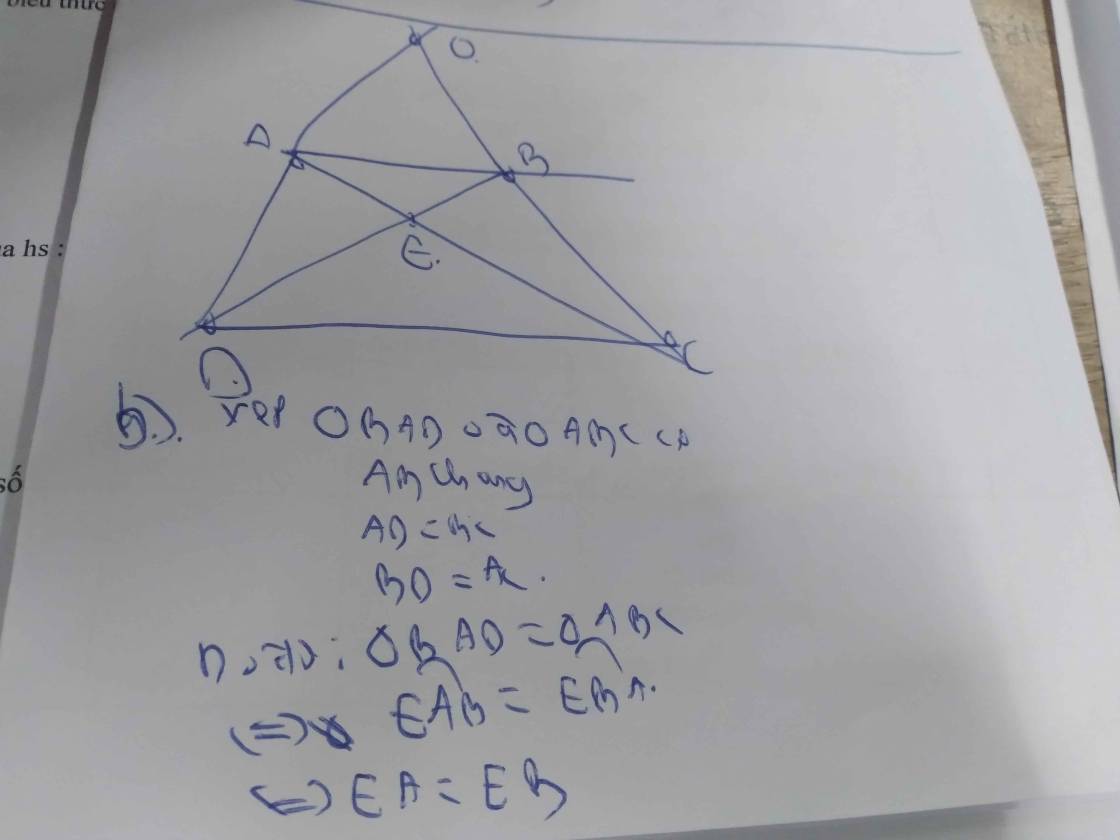
Cho hình thang cân ABCD (AB//CD, AB<CD). Gọi O là giao của AD và BC, gọi E là giao của AC và BD. CMR:
a) tam giác OAB cân
B) Tam giác ABD bằng tam giác BAC
C) EC=ED
D) OE là đường trung trực của AB và CD
Bài 4
Cho hình thang cân ABCD (AB//CD,AB<CD)
Gọi {O} = AD giao BC; {E} = AC giao BD. Chứng minh:
a) Tam giác AOB cân tại O
b) Tam giác ABD = Tam giác BAC
c) EC = ED
d) OE là trung trực chung của AB và CD
Cho hình thang cân ABCD có AB//CD , AB nhỏ hơn CD gọi O là giao điểm của AD và BC. E là giao điểm cua AC va BD
Cmr
Tam giác AOB cân tại O
Tam giác ABC = tam giác BAC
EC = ED
OE là trung trucchung của AB và CD
Mọi người ơi giúp mình bài này với.
Cho hình thang cân ABCD ( AB // CD ; AB < CD ) gọi O là giao điểm của 2 đường chéo AC và BD.
a) Chứng minh: tam giác AOB cân.
b) Chứng minh: OD = OC.
c) Gọi E là giao điểm AD và BC. Chứng minh: OE là trung trực của 2 đáy.
Bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tiaphân giác của BC · DBài 2: Cho hình thang cân ABCD (AB // CD, AB CD ). Gọi O là giao điểm của ADvà BC; Gọi E là giao điểm của AC và BD. Chứng minh:a) Tam giác AOB cân tại O;b) Các tam giác ABD và BAC bằng nhau;c) EC ED;d) OE là trung trực chung của AB và CD.Bài 3: Cho hình thang cân ABCD (AB // CD) có µ A C 2µ. Tính các góc của hình thang cânBài 4: Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạ...
Đọc tiếp
Bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia
phân giác của BC · D
Bài 2: Cho hình thang cân ABCD (AB // CD, AB < CD ). Gọi O là giao điểm của AD
và BC; Gọi E là giao điểm của AC và BD. Chứng minh:
a) Tam giác AOB cân tại O;
b) Các tam giác ABD và BAC bằng nhau;
c) EC = ED;
d) OE là trung trực chung của AB và CD.
Bài 3: Cho hình thang cân ABCD (AB // CD) có µ A C 2µ. Tính các góc của hình thang cân
Bài 4: Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên
BC và đồng thời DB là tia phân giác của ADC.
a) Tính các góc của hình thang cân ABCD.
b) Biết BC = 6 cm, tính chu vi và diện tích của hình thang cân ABCD.
Cho hình thang ABCD ( AB // CD). Gọi O là giao điểm của AC và BD. Qua O vẽ đường thẳng song song AB, CD cắt AD và BC lần lượt tại M và N
a) CM: O là trung điểm của MN
b) CM: 1/AB + 1/CD = 1/CM
c) CM: S tam giác OAD = S tam giác OBC
d) Gọi E là giao điểm của AD và BC. Gọi F là giao điểm của OE và CD. CM: F là trung điểm của CD
Cho hình thang cân ABCD ( AB // CD ) . Gọi O là giao điểm của AC và BD ; E là giao điểm của AD và BC .
a ) Chứng minh : Tam giác OCD cân
b ) Chứng minh : EO là đường trung trực của : AB ; CD
Cho hình thang cân ABCD, biết AB//CD. Gọi O là giao điểm của hai đường chéo AC và BD.
1) Chứng minh rằng tam giác AOB cân tại O.
2) Gọi M, N, P lần lượt là trung điểm của AD, BD và BC. Gọi E là giao điểm của AN với cạnh DC. Chứng minh rằng M, N, P thẳng hàng và tứ giác ADEB là hình bình hành.
3)Chứng minh rằng AB+BC+CD+DA/4<AC<AB+BC+CD+DA/2