a: Xét hình thang ABHK có
I là trung điểm của AK
IF//KH//AB
=>F là trung điểm của BH
=>BF=FH
Xét hình thang IFCD có
K là trung điểm của ID
KH//IF//CD
=>H là trung điểm của CF
=>HF=HC=BF
=>BH=2HC
b: AB=2*4-6=2cm
CD=2*6-4=8cm
Cho hình thang ABCD (AB//CD).Trên cạnh AD lấy hai điểm I và K sao cho AI=IK=KD.Từ I và K kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự tại F và H a) Chứng minh: BF=FH=HC b) Cho CD=8cm;IF=6cm. Tính AB và HK
Cho hình thang abcd(ab song song vs CD ) trên cạnh ad lấy 2 điểm i và k sao cho ai bằng ik bằng kd từ i và k kẻ các đường thẳng song song với đáy bc theo thứ tự tại f và h cm bf bằng fh bằng hc
cho CD bằng 8 if bằng 6 tính ab và hk
cho hình thang ABCD (AB//CD). Trên cạnh AD lấy hai điểm i vàK sao cho AI = IK =KD. Từ I và K kẻ các đường thẳng // vs 2 đáy cắt BC theo thứ tự tại F và H
a: cmr : BF=FH=HC
b: cho CD=8cm,IF=6CM TÍNH AB;HK
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Cho hình thang ABCD, đáy AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và AB tại F. Đường thẳng qua E, song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại M
a, Chứng minh bốn điểm M,N,P,Q nằm trên 1 đường thẳng song song với hai đáy
b, Chứng minh: MN = PQ
c, Cho AB=a, CD=b. Chứng minh rằng các điểm M, N,P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, DC theo cùng 1 tỉ số k. Tính k theo a và b.
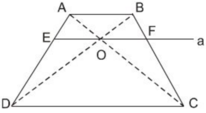
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
Cho hình thang cân ABCD (AB//CD; AB<CD). Qua A kẻ đường thẳng song song với BC cắt CD tại M.
a, Tứ giác ABCM hình gì? Vì sao?
b, Gọi I;H và K theo thứ tự là trung điểm của AM, AC và BC. Chứng minh H là trung điểm của IK
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
