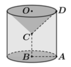
Thể tích khối tròn xoay tạo thành bằng thể tích hình trụ có bán kính đáy AB và đường sinh AD trừ đi phần thể tích hình nón có bán kính đáy OD = AB và đường cao OC = AD - BC
Vậy ![]()
Chọn B.

Thể tích khối tròn xoay tạo thành bằng thể tích hình trụ có bán kính đáy AB và đường sinh AD trừ đi phần thể tích hình nón có bán kính đáy OD = AB và đường cao OC = AD - BC
Vậy ![]()
Chọn B.
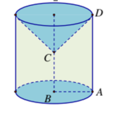
Cho hình thang ABCD vuông tại A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 π a 3 3
B. V = 5 π a 3 3
C. V = π a 3
D. V = 7 π a 3 3
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho hình thang cân ABCD có các cạnh AB=2a, CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A. V = 4 3 π a 3
B. V = 4 + 10 2 3 π a 3
C. V = 10 2 3 π a 3
D. V = 14 2 3 π a 3
Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
A. V = 4 3 πa 3
B. V = 4 + 10 2 3 πa 3
C. V = 10 2 3 πa 3
D. V = 14 2 3 πa 3
Cho hình thang ABCD vuông tại A và B, BC=2AB=2AD=2a. Thể tích của khối tròn xoay tạo thành khi quay hình thang ABCD quanh cạnh AB là
A. 7 π a 3 3
B. 7 π a 3
C. π a 3 3
D. 7 π a 3 2
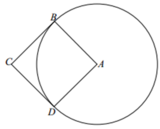
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC.
A. 1000 π + 375 π 2 6
B. 1000 π + 375 π 2 6
C. 500 π + 125 π 2 6
D. 500 π + 375 π 2 6
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Giả sử một hình thang cong giới hạn bởi đồ thị hàm số y = f x , trục Ox và hai đường thẳng x=a và x=b (a<b) quay xung quanh trục Ox tạo thành một khối tròn xoay. Viết công thức tính thể tích V của khối tròn xoay đó.
A. V = π ∫ b a f 2 x d x
B. V = ∫ a b f x d x
C. V = π ∫ a b f 2 x d x
D. V = ∫ a b f 2 x d x
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB= a, E F B ^ = 30 ° và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
A. V = 4 / 3 a 3
B. V= 10/9 a 3
C. V= 4/3 π a 3
D. V= 10/9 π a 3