Question

Cho hình thang ABCD với hai đáy là AB và CD thòa mãn AB + CD = AD. Hai đường chéo AC và BD cắt nhau tại E , qua E kẻ đường thẳng song song AB cắt AD tại F . CMR góc BFC = 90 độ

Answer 1

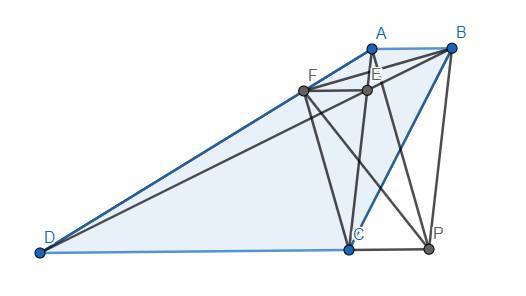
 Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)

 Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)

 \(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)

\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)

 Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)