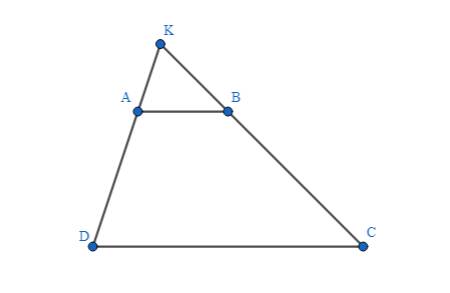
a, Vì tứ giác \(ABCD\) là hình thang có hai đáy là \(AB\) và \(CD\) (gt)
\(\Rightarrow AB//CD\) (t/c)
Xét \(\Delta KDC\) có: \(AB//CD\) (cmt) \(\Rightarrow\dfrac{KA}{KD}=\dfrac{AB}{CD}\) (hệ quả đli Talet)
Mà \(\dfrac{AB}{CD}=\dfrac{1}{3}\) (vì \(AB=\dfrac{1}{3}CD\)) nên \(\dfrac{KA}{KD}=\dfrac{1}{3}\)
Vậy \(\dfrac{KA}{KD}=\dfrac{1}{3}\).
b, Vì \(AB//CD\) (cmt) \(\Rightarrow\widehat{KAB}=\widehat{KDC}\) (2 góc đồng vị)
Xét \(\Delta KAB\) và \(\Delta KDC\) có: \(\left\{{}\begin{matrix}\widehat{K}\text{ chung}\\\widehat{KAB}=\widehat{KDC}\text{ (cmt)}\end{matrix}\right.\)
\(\Rightarrow \Delta KAB\backsim\Delta KDC\text{ (g.g) }\)
\(\Rightarrow\dfrac{S_{\Delta KAB}}{S_{\Delta KDC}}=\left(\dfrac{AB}{CD}\right)^2=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\) (theo t/c và vì \(\dfrac{AB}{CD}=\dfrac{1}{3}\))
\(\Rightarrow S_{\Delta KDC}=S_{\Delta KAB}\cdot9=6\cdot9=54\left(cm^2\right)\) (vì \(S_{\Delta KAB}=6cm^2\))
Khi đó: \(S_{ABCD}=S_{\Delta KDC}-S_{\Delta KAB}=54-6=48\left(cm^2\right)\)
Vậy \(S_{ABCD}=48cm^2\).
P/s: Có vẻ đây không phải 1 bài toán lớp 5, bạn xem lại nhé.