Các câu hỏi tương tự
Số phát biểuđúng:1. Qua phép vị tự có tỉ số
k
≠
0
, đường thẳng đi qua tâm vị tự sẽ biến thành chính nó2. Qua phép vị tự có tỉ số
k
≠
0
, đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.3. Qua phép vị tự có tỉ số
k
≠
1
, không có đường tròn nào biến thành chính nó.4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song so...
Đọc tiếp
Số phát biểuđúng:
1. Qua phép vị tự có tỉ số k ≠ 0 , đường thẳng đi qua tâm vị tự sẽ biến thành chính nó
2. Qua phép vị tự có tỉ số k ≠ 0 , đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.
3. Qua phép vị tự có tỉ số k ≠ 1 , không có đường tròn nào biến thành chính nó.
4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.
5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó
6. Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với hệ số k
7. Trong phép vị tự tâm O, tỉ số k, nếu k < 0 thì điểm M và ảnh của nó ở về hai phía đối với tâm O.
8. Mọi phép dời hình đều là phép đồng dạng với tỉ số k = 1
9. Phép hợp thành của một phép vị tự tỉ số k và một phép đối xứng tâm là phép đồng dạng tỉ số
10. Hai đường tròn bất kì luôn có phép vị tự biến đường này thành đường kia
11. Khi k = 1 , phép vị tự là phép đồng nhất
12. Phép vị tự biến tứ giác thành tứ giác bằng nó
13. Khi k = 1, phép đồng dạng là phép dời hình
14. Phép đối xứng tâm là phép đồng dạng tỉ số k = 1
A.9
B.10
C.11
D.12
Cho hình chóp S.ABCD có đáy ABCD là hình thang,AD là đáy lớn và AD 2BC . Gọi M, N lần lượt là trung điểm của SB, SC, O AC BD .
a) Tìm giao tuyến của ABN và SCD.
b) Tìm giao điểm P của DN và SAB .
c) Gọi K AN DM . Chứng minh 3 điểm S, K, O thẳng hàng. Tính KS KO .
Cho hình chóp có đáy là hình thang SABCD ,sao cho AB=3DC và AB // CD . Gọi O là giao điểm của AC và BD , K là điểm trên cạnh SB sao cho 2SK=KB , I là điểm trên cạnh AB sao cho BI=2/3 BA . 1. Chứng minh IK//(SAC) 2. Gọi E là giao điểm AD của BC và . Chứng minh: SE//CK
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
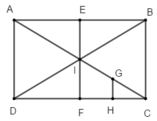
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k2 và phép đối xứng tâm I biến tứ giác IGHF thành A. AIFD B. BCFI C. CIEB D. DIEA
Đọc tiếp
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k=2 và phép đối xứng tâm I biến tứ giác IGHF thành
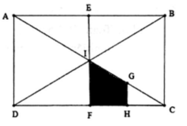
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho đường tròn (C), tâm O, có bán kính 4, phép vị tự tâm O tỉ số k= –2 biến (C) thành (C’) có bán kính bằng bao nhiêu:
A. 2
B. 4
C.8
D. 16
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + 3y - 3 = 0. Ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 biến đường thẳng d thành đường thẳng có phương trình là:
A. 2x + 3y - 6 = 0
B. 4x + 6y - 5 = 0
C. -2x - 3y + 3 = 0
D. 4x + 6y - 3 = 0
Cho hình chóp S ABCD . có đáy ABCD là hình bình hành tâm O. Gọi M.N.P lần lượt là trung điểm AD,BC và SB a, tìm giao điểm Q của SA và (MNP) b, chứng minh SD//(MNP) và (SMC)//(ANP) c, gọi H=BD ∩ AN, K=BD ∩ MC, i= PK ∩ SH. tính tỉ số SΔSLK/SΔSLP
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. BD lần lượt cắt CE, AF lần lượt tại K và H. Phép vị tự tâm H tỉ số k biến D thành B. Khi đó k bằng:
A. 2
B. -2
C. 1 2
D. − 1 2