Question

Cho hình chóp S ABCD . có đáy ABCD là hình bình hành tâm O. Gọi M.N.P lần lượt là trung điểm AD,BC và SB a, tìm giao điểm Q của SA và (MNP) b, chứng minh SD//(MNP) và (SMC)//(ANP) c, gọi H=BD ∩ AN, K=BD ∩ MC, i= PK ∩ SH. tính tỉ số SΔSLK/SΔSLP

Answer 1

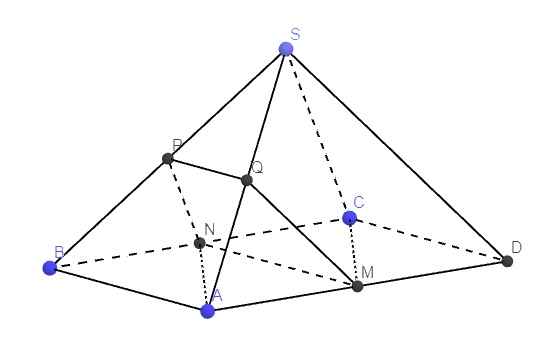
a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)

Gọi Q là trung điểm SA

\(\Rightarrow PQ\) là đường trung bình tam giác SAB

\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)

\(\Rightarrow Q=SA\cap\left(MNP\right)\)

b. Do Q là trung điểm SA, M là trung điểm AD

\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)

Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)

Tương tự ta có \(NP||SC\) (đường trung bình) (1)

\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)

(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)

c. Đề bài không tồn tại điểm L

Answer 2