Chọn đáp án A.
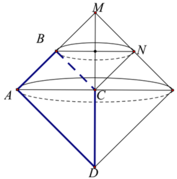
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
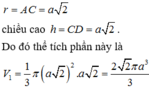

Chọn đáp án A.

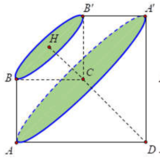
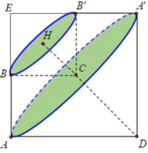
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
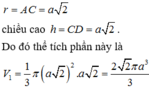



Cho hình thang ABCD có ∠ A = ∠ B = 90 0 , A B = B C = a , A D = 2 a . Tính thể tích khối nón tròn xoay sinh ra khi quay quanh hình thang ABCD xung quanh trục CD
A. 7 π a 3 12
B. 7 2 π a 3 12
C. 7 2 π a 3 6
D. 7 π a 3 6
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB = AD = 2 cm , CD = 2 AB . Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB
A. 40 π 3 cm 3
B. 16 π 3 cm 3
C. 8 πcm 3
D. 8 π 3 cm 3
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho hình thang vuông ABCD có A ⏞ = D ⏞ = 90 ∘ , AB=AD=2, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
A. 8 π cm 3
B. 40 π 3 c m 3
C. 8 π 3 c m 3
D. 16 π 3 c m 3
Cho hình thang ABCD vuông tại A và D, cạnh AB=AD=a và DC=2a. Thể tích khối tròn xoay sinh ra khi hình thang ABCD quay quanh trục AD là
A. 5 πa 3 3
B. 7 πa 3 3
C. 8 πa 3 3
D. 4 πa 3 3
Cho hình thang cân ABCD có các cạnh AB=2a, CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A. V = 4 3 π a 3
B. V = 4 + 10 2 3 π a 3
C. V = 10 2 3 π a 3
D. V = 14 2 3 π a 3
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh S x q của khối K
A. S x q = πa 2 2
B. S x q = 3 πa 2 2
C. S x q = 3 πa 2
D. S x q = πa 2
Cho một hình thang cân ABCD có cạnh đáy A B = 2 a , C D = 4 a , cạnh bên A D = B C = 3 a . Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
A. 4 2 π a 3 3
B. 56 2 π a 3 3
C. 16 2 π a 3 3
D. 14 2 π a 3 3
Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
A. V = 4 3 πa 3
B. V = 4 + 10 2 3 πa 3
C. V = 10 2 3 πa 3
D. V = 14 2 3 πa 3