Các câu hỏi tương tự
Cho hình thang ABCD có AB song song với CD. Cho AB2a và CD a. Gọi O là trung điểm của AD. Khi đó: A. B. C. D.
Đọc tiếp
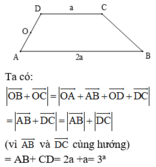
Cho hình thang ABCD có AB song song với CD. Cho AB=2a và CD= a. Gọi O là trung điểm của AD. Khi đó:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và ABCD.M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E2) Giả sử EA tiếp xúc (O). Chứng minh rằng khi đó QM vuông góc với CD.
Đọc tiếp
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và AB<CD.M là trung điểm CD.
P là điểm di chuyển trên đoạn MD ( P khác M, D ).AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B,
QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E
2) Giả sử EA tiếp xúc (O). Chứng minh rằng khi đó QM vuông góc với CD.
Cho tứ giác ABCD,gọi m,N lần lượt là trung điểm của AD,BC.Biết AB=CD=2a và MN=a\(\sqrt{3}\)
a)CMR: AB không song song với CD
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và ABCD.M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.
Đọc tiếp
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và AB<CD.
M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).
AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E
1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.
Cho hình thang vuông ABCD vuông tại A,D với AB=AD=a, CD=2a gọi O là giao điểm của AC và BD. Tím độ dài các vt OC, vt OB
cho hình thang ABCD có 2 đáy AB=a, CD = 2a Gọi M, N là trung điểm AD và BC Khi đó \(|\overrightarrow{MA}+\overrightarrow{MC}-\overrightarrow{MN}|\) bằng:
Cho hình thang vuông ABCD có đường cao AB 2a, đáy lớn BC 3a, đáy nhỏ AD a. Gọi I là trung điểm của CD. Tìm mệnh đề đúng? A. Góc AIB là góc vuông B. Tam giác BIC là tam giác vuông C. AI và BD vuông góc với nhau D. Tất cả sai
Đọc tiếp
Cho hình thang vuông ABCD có đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = a. Gọi I là trung điểm của CD. Tìm mệnh đề đúng?
A. Góc AIB là góc vuông
B. Tam giác BIC là tam giác vuông
C. AI và BD vuông góc với nhau
D. Tất cả sai
Cho hình thang vuông ABCD có đáy lớn AB 4a, đáy nhỏ CD 2a, đường cao AD 3a; I là trung điểm của AD . Khi đó
I
A
→
+
I
B
→
.
I
D
→
bằng : A. B. C. 0 D. 9a2
Đọc tiếp
Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD . Khi đó I A → + I B → . I D → bằng :
A. ![]()
B. ![]()
C. 0
D. 9a2
Cho hình thang ABCD có hai đáy là AB = a và CD = 2a; gọi M, N lần lượt là trung điểm của AD và BC. Tính MA MC MN theo a.