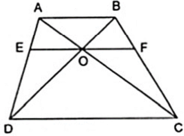
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
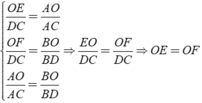
Điều phải chứng minh.

Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
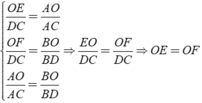
Điều phải chứng minh.
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
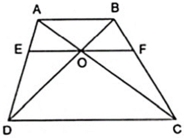
Cho hình thang ABCD (AB// CD) có O là giao điểm 2 đường chéo. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại E và H. Chứng minh OE= OH.
Cho hình thang ABCD có AB //CD có O là giao điểm 2 đường chéo qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại E và H chứng minh OE=OH
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
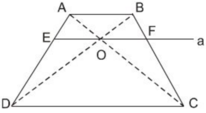
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F
Chứng minh rằng OE = OF.
Cho hình thang ABCD , AB//CD. Qua giao điểm O của 2 đường chéo, hai đường thẳng song song với 2 đáy, cắt AD và BC lần lượt ở E và H. CM: OE=OH
Cho hình thang ABCD ( AB//CD), Gọi M,N lần lượt là trung điểm của AB<CD, O là giao điểm của AC và BD; I là giao điểm của AD,BC
a) chứng minh O,I,M,N thẳng hàng
b) Qua O kẻ đường thẳng song song với AB cắt AD,BC lần lượt tại E,F. Chứng minh OE=OF
Cho hình thang ABCD (AB//CD). Hai đường chéo AC và BDcắt nhau tại O . đường thẳng A đi qua O và song song với đáy của hình thang cách các cạnh bên AD,BC theo thứ tự tại E và F chứng minh rằng OE=OF
Cho hinh thang ABCD(AB//CD), đường thẳng song song với hai đáy lần lượt cắt AD,AC,BD,BC tại I,K,M,N
a.Chứng minh IK=MN
b.Đường thẳng đi qua giao điểm O của hai đương chéo và song song với hai đáy cắt cạnh bên ở E,F. C/M:OE=OF