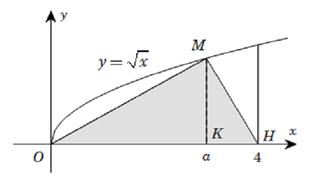
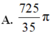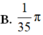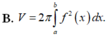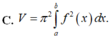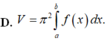Để tính thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2-10x+24\), trục hoành và các đường thẳng \(x=-1;x=0\) quay quanh trục \(Ox\), ta sử dụng công thức tính thể tích khối tròn xoay:
\(V=\pi\int\limits^0_{-1}\left(x^2-10x+24\right)^2dx\)
\(\Rightarrow V=\pi\int\limits^0_{-1}\left(x^4-20x^3+148x^2-480x+576\right)dx\)
\(\Rightarrow V=\pi\left[\dfrac{x^5}{5}-5x^4+\dfrac{148x^3}{3}-240x^2+576x\right]^0_{-1}\)
\(\Rightarrow V=\pi\left[0-\left(-\dfrac{1}{5}-5-\dfrac{148}{3}-240-576\right)\right]\)
\(\Rightarrow V=\pi\left[0-\left(-\dfrac{13058}{15}\right)\right]=\dfrac{13058\pi}{15}\left(đvtt\right)\)
.
(đvtt).
(đvtt).
(đvtt).
(đvtt).
