Các câu hỏi tương tự
Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
a) Tính diện tích xung quanh của hình nón đã cho.
b) TÍnh thể tích của khối nón được tạo bởi hình nón đó.
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.
Cho hình nón tròn xoay có đường cao
h
40
(
c
m
)
, bán kính đáy
r
50
c
m
. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là
24
(
c
m
)
. Tính diện tích của thiết diện A. S800
c
m
2...
Đọc tiếp
Cho hình nón tròn xoay có đường cao h = 40 ( c m ) , bán kính đáy r = 50 c m . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 ( c m ) . Tính diện tích của thiết diện
A. S=800 c m 2
B. S=1200 c m 2
C. S=1600 c m 2
D. S=2000 c m 2
Chia tấm bìa hình tròn bán kính R30 cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là: A.
2
π
R
3
2
81
B.
π
R
3
27
C...
Đọc tiếp
Chia tấm bìa hình tròn bán kính R=30 cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là:
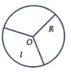
A. 2 π R 3 2 81
B. π R 3 27
C. 2 π R 3 2 27
D. π R 3 81
Cho khối nón tròn xoay có đường cao h 20cm, bán kính đáy r 25cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng: A.
500
c
m
2
B.
475
c
m
2
C.
450
c
m
2
D.
550...
Đọc tiếp
Cho khối nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng:
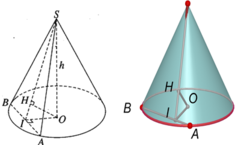
A. 500 c m 2
B. 475 c m 2
C. 450 c m 2
D. 550 c m 2
Hình nón tròn xoay có chiều cao
h
3
a
,
bán kính đường tròn đáy
r
a
.
Thể tích khối nón bằng A.
3
π
a
3
B.
π
a
3
9
C.
π
a
3
D.
π...
Đọc tiếp
Hình nón tròn xoay có chiều cao h = 3 a , bán kính đường tròn đáy r = a . Thể tích khối nón bằng
A. 3 π a 3
B. π a 3 9
C. π a 3
D. π a 3 3
Cho một khối cầu tâm O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng x (cm) cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng A. 2cm B. 3cm. C. 4cm D. 0cm
Đọc tiếp
Cho một khối cầu tâm O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng x (cm) cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng
A. 2cm
B. 3cm.
C. 4cm
D. 0cm
Cho hình nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R. Diện tích toàn phần của hình nón bằng A.
2
πR
(
l
+
R
)
B.
πR
(
l
+
R
)
C.
πR
(
2
l
+
R
)
D.
πR
(
l
+
2...
Đọc tiếp
Cho hình nón tròn xoay có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R. Diện tích toàn phần của hình nón bằng
A. 2 πR ( l + R )
B. πR ( l + R )
C. πR ( 2 l + R )
D. πR ( l + 2 R )
Từ một khúc gỗ dạng khối nón tròn xoay có thể tích bằng
343
3
π
c
m
3
và chu vi đường tròn đáy bằng
14
π
c
m
. Trong sản xuất, người ta muốn tạo ra một vật thể có hình dạng khối cầu (S) từ khối gỗ trên. Gọi S là diện tích mặt cầu (S). Tính giá trị lớn nhất của diện tích S A.
196
π
3
−...
Đọc tiếp
Từ một khúc gỗ dạng khối nón tròn xoay có thể tích bằng 343 3 π c m 3 và chu vi đường tròn đáy bằng 14 π c m . Trong sản xuất, người ta muốn tạo ra một vật thể có hình dạng khối cầu (S) từ khối gỗ trên. Gọi S là diện tích mặt cầu (S). Tính giá trị lớn nhất của diện tích S
A. 196 π 3 − 2 2 c m 2
B. 196 π 6 − 4 2 c m 2
C. 196 π c m 2
D. 196 π 2 c m 2
Một hình thang vuông ABCD có đường cao
A
D
π
, đáy nhỏ
A
B
π
, đáy lớn
C
D
2
π
. Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng: A.
4
3
π
4
B.
7
3
π
4
C.
10
3...
Đọc tiếp
Một hình thang vuông ABCD có đường cao A D = π , đáy nhỏ A B = π , đáy lớn C D = 2 π . Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4