HD: Gọi r, h lần lượt là bán kính đáy, chiều cao của hình trụ
Hình trụ nội tiếp hình nón ![]() (tam giác đồng dạng)
(tam giác đồng dạng)

HD: Gọi r, h lần lượt là bán kính đáy, chiều cao của hình trụ
Hình trụ nội tiếp hình nón ![]() (tam giác đồng dạng)
(tam giác đồng dạng)

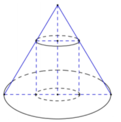
Cho hình nón có chiều cao 2R và bán kính đường tròn đáy R. Xét hình trụ nội tiếp hình nón sao cho có thể tích khối trụ lớn nhất, khi đó bán kính đáy của khối trụ bằng:
A. 2 R 3
B. R 3
C. 3 R 4
D. R 2
Cho khối trụ có hai đáy là hai hình tròn (O) và (O’), chiều cao bằng R 3 và bán kính đáy là R. Một hình nón có đỉnh là (O’) và đáy là hình tròn (O;R). Tỷ số diện tích xung quanh của hình trụ và hình nón bằng:
A. 3.
B. 2
C. 2.
D. 3
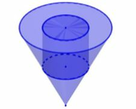
Một bình đựng nước dạng hình nón (không có nắp đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài 16 π 9 ( d m 3 ) . Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (như hình vẽ). Tính bán kính đáy R của bình nước.
A. R = 4(dm)
B. R = 3(dm)
C. R = 5(dm)
D. R = 2(dm)
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h = 1 , 5 m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R = 1 m và có chiều cao bằng 1 3 h ;
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
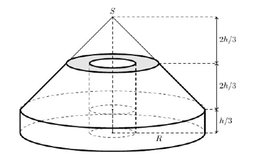
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
A. 2 , 815 m 3
B. 2 , 814 m 3
C. 3 , 403 m 3
D. 3 , 109 m 3
Cho hình nón (N) có bán kính r = 20(cm), chiều cao h = 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
A. V=3000 π ( cm 3 ) .
B. V= 32000 9 π ( cm 3 ) .
C. V=3600 π ( cm 3 ) .
D. V=4000 π ( cm 3 ) .
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L). Dựng hình trụ có một đáy là đường tròn (L), một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất
A. x = h 2
B. x = h 3
C. x = h 4
D. x = h
Cho hình trụ có hai đáy là hai hình tròn (O) và (O') chiều cao bằng R 3 và bán kính đáy R. Một hình nón có đỉnh là O' và đáy là hình tròn (O; R). Tỷ số diện tích xung quanh của hình trụ và hình nón bằng
A. 3
B. 2
C. 2
D. 3