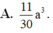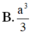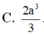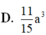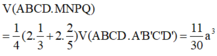Các câu hỏi tương tự
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, một mặt phẳng
α
cắt các cạnh
A
A
,
B...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, một mặt phẳng α cắt các cạnh A A ' , B B ' , C C ' , D D ' lần lượt tại M , N , P , Q . Biết A M = 1 3 a , C P = 2 5 a . Thể tích khối đa diện ABCD.MNPQ là
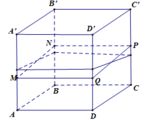
A. 11 30 a 2
B. a 3 3
C. 2 a 3 3
D. 11 15 a 3
Cho hình lập phương ABCD. ABCD có cạnh bằng a, một mặt phẳng cắt các cạnh AA, BB, CC, DD lần lượt tại M, N, P, Q. Biết AM
1
3
a
, CP
2
5
a
. Thể tích khối đa diện ABCD.MNPQ là
Đọc tiếp
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a, một mặt phẳng cắt các
cạnh AA', BB', CC', DD' lần lượt tại M, N, P, Q. Biết AM= 1 3 a , CP= 2 5 a .
Thể tích khối đa diện ABCD.MNPQ là
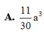
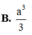
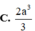
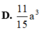
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh
A
B
và sao cho
M
A
M
B
và
N
B
2
N
C
. Mặt phẳng
D
M...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và sao cho M A ' = M B ' và N B = 2 N C . Mặt phẳng D M N chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A , V H ' là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
Cho hình lăng trụ đều ABCD.ABCD có đáy là hình vuông cạnh a. Mặt phẳng
α
lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng
α
và mặt phẳng (ABCD) là
60
0
. Diện tích tứ giác MNPQ là :
Đọc tiếp
Cho hình lăng trụ đều ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Mặt phẳng α lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng α và mặt phẳng (ABCD) là 60 0 . Diện tích tứ giác MNPQ là :
![]()
![]()
![]()
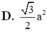
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Cho hình lập phương ABCD.ABCD có cạnh bằng
3
. Mặt phẳng
α
cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng
α
biết
α
tạo với mặt (ABBA) một góc
60
0
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 . Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt (ABB'A') một góc 60 0 .
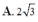
![]()
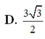
Cho hình lập phương ABCD.ABCD cạnh 2a, gọi M là trung điểm của BB và P thuộc cạnh sao cho
D
P
1
4
D
D
. Mặt phẳng (AMP) cắt CC tại N. Thể tích khối đa diện AMNPBCD bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng

![]()
![]()
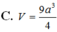

Cho hình lập phương ABCD.ABCD cạnh a. Gọi M , N, P lần lượt là trung điểm các cạnh CD, AB, AD . Thể tích khối tứ diện A MNP bằng: A.
a
3
16
B.
a
3
32
C.
a
3
12
D.
a
3
24
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M , N, P lần lượt là trung điểm các cạnh CD, A'B', A'D' . Thể tích khối tứ diện A' MNP bằng:
A. a 3 16
B. a 3 32
C. a 3 12
D. a 3 24
Cho hình chóp S.ABCD có đáy là hình vuông cạnh
2
2
, cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng
(
α
)
qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy. Mặt phẳng ( α ) qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP bằng
![]()
![]()
![]()
![]()