Đáp án A
Thể tích của khối đa diện ABCD.MNPQ bằng thể tích khối hình hộp đứng có đáy là
ABCd và chiều cao h = 1 2 ( a 3 + 2 a 5 ) = 11 a 30
Vậy thể tích cần tính V = 11 30 a 3
Đáp án A
Thể tích của khối đa diện ABCD.MNPQ bằng thể tích khối hình hộp đứng có đáy là
ABCd và chiều cao h = 1 2 ( a 3 + 2 a 5 ) = 11 a 30
Vậy thể tích cần tính V = 11 30 a 3
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, một mặt phẳng α cắt các cạnh M.N,P,Q lần lượt tại M, N, P, Q. Biết A M = 1 3 a , C P = 2 5 a . Thể tích khối đa diện ABCD.MNPQ là
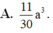
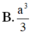
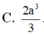
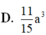
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a, một mặt phẳng cắt các
cạnh AA', BB', CC', DD' lần lượt tại M, N, P, Q. Biết AM= 1 3 a , CP= 2 5 a .
Thể tích khối đa diện ABCD.MNPQ là
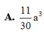
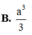
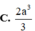
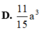
Cho hình chóp S.ABC có SA=a, SB=b, SC=c. Một mặt phẳng (α) đi qua trọng tâm của tam giác ABC, cắt các cạnh SA, SB, SC lần lượt tại A’, B’, C’. Tìm giá trị nhỏ nhất của 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2
A. 3 a 2 + b 2 + c 2 .
B. 2 a 2 + b 2 + c 2 .
C. 2 a 2 + b 2 + c 2 .
D. 9 a 2 + b 2 + c 2 .
Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng
A. 2 3
B. - 2 3
C. 5 3
D. - 5 3
Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt phẳng qua A vuông góc với SC cắt SB, SC lần lượt tại M, N. Biết rằng SA = AC = 5, AB = 3, BC = 4. Thể tích khối chóp S.AMN bằng:
A. 125 68 B. 125 34
C. 175 34 D. 125 17