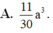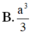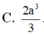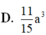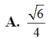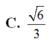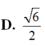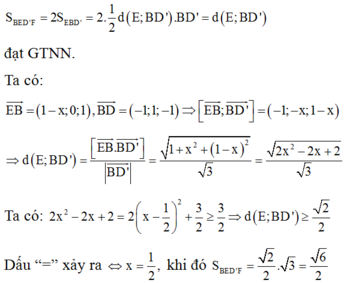Các câu hỏi tương tự
Cho hình lập phương ABCD.ABCD có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được. A. 4 B. 4
2
C.
6
D.
2
6
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được.
A. 4
B. 4 2
C. 6
D. 2 6
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, AB và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng A.
10
4
B.
6
3
C. ...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, A'B' và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng
A. 10 4
B. 6 3
C. 6 6
D. 3 3
Cho hình lập phương ABCD.ABCD cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
![]()
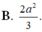
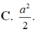

Cho hình lập phương ABCD.ABCD có cạnh bằng
3
. Mặt phẳng
α
cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng
α
biết
α
tạo với mặt (ABBA) một góc
60
0
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 . Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt (ABB'A') một góc 60 0 .
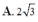
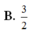
![]()
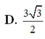
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A' Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
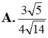
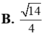
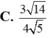
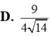
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
. Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD. Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 . Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D'. Khi đó
![]()
![]()
![]()
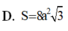
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
![]()
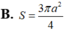
![]()
![]()
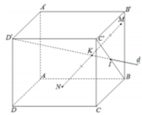
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
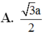
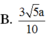
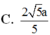
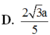
Cho hình lập phương ABCD.ABCD có cạnh bằng a, một mặt phẳng
α
cắt các cạnh M.N,P,Q lần lượt tại M, N, P, Q. Biết
A
M
1
3
a
,
C
P
2
5
a
. Thể tích khối đa diện ABCD.MNPQ là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, một mặt phẳng α cắt các cạnh M.N,P,Q lần lượt tại M, N, P, Q. Biết A M = 1 3 a , C P = 2 5 a . Thể tích khối đa diện ABCD.MNPQ là