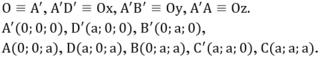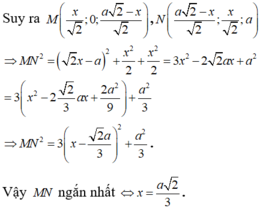Các câu hỏi tương tự
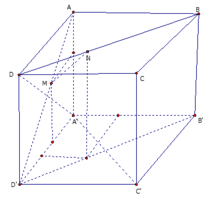
Cho hình lập phương ABCD.ABCD cạnh bằng a. Lấy điểm M thuộc đoạn AD¢, điểm N thuộc đoạn BD sao cho AMDNx với
0
x
a
2
2
. Tìm x theo a để đoạn MN ngắn nhất
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD¢, điểm N thuộc đoạn BD sao cho AM=DN=x với 0 < x < a 2 2 . Tìm x theo a để đoạn MN ngắn nhất
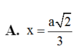
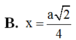
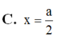
![]()
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB 2a, AD a. Gọi K là điểm thuộc BC sao cho
3
B
K
→
+
2
C
K
→
0
→
Tính khoảng cách giữa hai đươ...
Đọc tiếp
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB = 2a, AD = a. Gọi K là điểm thuộc BC sao cho 3 B K → + 2 C K → = 0 → Tính khoảng cách giữa hai đường thẳng AD và SK.
A . x = 2 165 a 15
B . x = 165 a 15
C . x = 2 135 a 15
D . x = 135 a 15
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
m
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S m ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - m ) 2 = m 2 4 và hai điểm A(2;3;5), B(1;2;4). Tìm giá trị nhỏ nhất của m để trên ( S m ) tồn tại điểm M sao cho M A 2 - M B 2 = 9 .
A. m=1
B. m= 3 - 3
C. m= 8 - 4 3
D. m= 4 - 3 2
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình vuông cạnh a. Các điểm M, N lần lượt nằm trên AD', DB sao cho AM = DN = x; (0 < x < a 2 ). Khi x thay đổi, đường thẳng MN luôn song song với mặt phẳng cố định nào sau đây?
A. (CB'D')
B. (A'BC)
C. (AD'C)
Cho hàm số y f(x) thỏa mãn f(-2) -2, f(2) 2 và có bảng biến thiên như hình bên Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình
f
-
f
x
≥
≥
m
có nghiệm thuộc đoạn [-1;1]? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn f(-2) = -2, f(2) = 2 và có bảng biến thiên như hình bên
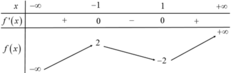
Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình f - f x ≥ ≥ m có nghiệm thuộc đoạn [-1;1]?
A. 1.
B. 2.
C. 3.
D. 4.
Cho phương trình z^2+bc+c0 có hai nghiệm z1 z2 thỏa mãn z2 - z1 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình z^2-2bz+4c0 . Tính độ dài đoạn ABA: 8sqrt{5}B: 2sqrt{5}C: 4sqrt{5}D: sqrt{5}
Đọc tiếp
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) (x-6)
x
2
+
4
trên đoạn [0;3] có dạng a - b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b + c. A. 4 B. -2 C. -22 D. 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác A’BD. Tìm thể tích khối tứ diện GABD
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi G là trọng tâm tam giác A’BD. Tìm thể tích khối tứ diện GABD
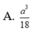
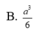
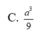
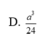
Trong không gian Oxyz cho hai mặt phẳng (P): x-y+2z-30, (Q): x-y+2z+30 có bao nhiêu điểm M có hoành độ nguyên thuộc Ox sao cho tổng khoảng cách từ M đến hai mặt phẳng (P), (Q) bằng khoảng cách giữa (P) và (Q). A. 2 B. 4 C. 6 D. 7
Đọc tiếp
Trong không gian Oxyz cho hai mặt phẳng (P): x-y+2z-3=0, (Q): x-y+2z+3=0 có bao nhiêu điểm M có hoành độ nguyên thuộc Ox sao cho tổng khoảng cách từ M đến hai mặt phẳng (P), (Q) bằng khoảng cách giữa (P) và (Q).
A. 2
B. 4
C. 6
D. 7