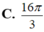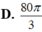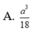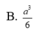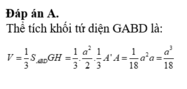Các câu hỏi tương tự
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và ABCD là hình vuông cạnh a, góc giữa SC và mặt phẳng (ABCD) bằng
45
∘
. Mặt phẳng (
α
) qua A và vuông góc với SC và chia khối chóp S.ABCD thành hai khối đa diện. Gọi
V
1
là thể tích của khối đa diện có chứa điểm S và
V
2
là thể tích của khối đa...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và ABCD là hình vuông cạnh a, góc giữa SC và mặt phẳng (ABCD) bằng 45 ∘ . Mặt phẳng ( α ) qua A và vuông góc với SC và chia khối chóp S.ABCD thành hai khối đa diện. Gọi V 1 là thể tích của khối đa diện có chứa điểm S và V 2 là thể tích của khối đa diện còn lại. Tìm tỉ số V 1 V 2 ?
A. 1
A. 1 3
C. 1 2
D. 4 5
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. A.
5
π
15
18
B.
5
π
15
54...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
A. 5 π 15 18
B. 5 π 15 54
C. 4 π 3 27
D. 5 π 3
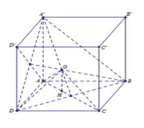
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
11
a
2
2
là mặt cầu
Đọc tiếp
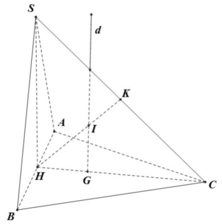
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn M A 2 + M B 2 + M C 2 + M D 2 = 11 a 2 2 là mặt cầu
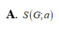
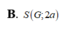
![]()
![]()
Cho hình chóp đều n cạnh (n
≥
3). Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng
60
∘
, thể tích khối chóp bằng
3
3
4
R
2
. Tìm n? A. n 4 B. n 8 C. n 10 D. n 6
Đọc tiếp
Cho hình chóp đều n cạnh (n ≥ 3). Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60 ∘ , thể tích khối chóp bằng 3 3 4 R 2 . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
Cho tứ diện đều có cạnh bằng 3. M là một điểm thuộc miền trong của khối tứ diện tương ứng. Tính giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt của tứ diện đã cho. A. 36 B. 9/64 C.
6
D.
6
4
Đọc tiếp
Cho tứ diện đều có cạnh bằng 3. M là một điểm thuộc miền trong của khối tứ diện tương ứng. Tính giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt của tứ diện đã cho.
A. 36
B. 9/64
C. 6
D. 6 4
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
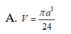
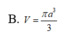
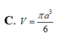
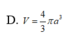
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng
a
3
4
. Tính thể tích của khối chóp đã cho theo a. A.
a
3
3
4...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng a 3 4 . Tính thể tích của khối chóp đã cho theo a.
A. a 3 3 4
B. a 3 3 2
C. a 3 3 6
D. a 3 3 12
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB 3a, AA’ 6a. A.
V
7
a
3
B.
V
6
2
a
3...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 7 a 3
B. V = 6 2 a 3
C. V = 8 a 3
D. V = 6 a 3
Cho hình nón có bán kính đáy r4 và diện tích xung quanh bằng 20
π
. Thể tích của khối nón đã cho bằng
Đọc tiếp
Cho hình nón có bán kính đáy r=4 và diện tích xung quanh bằng 20 π . Thể tích của khối nón đã cho bằng
![]()
![]()