Các câu hỏi tương tự
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là: A.
S
π
a
2
B.
S
3
π
a
2
4
C.
S...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
A. S = π a 2
B. S = 3 π a 2 4
C. S = 3 π a 2
D. S = 12 π a 2
Tính diện tích S của mặt cầu ngoại tiếp hình lập phương cạnh bằng 2
A. S = 8 π 3
B. S = 48 π
C. S = 2 π 3
D. S = 12 π
Cho hình lập phương cạnh a nội tiếp mặt cầu (S). Tính diện tích mặt cầu (S). A.
π
a
2
B.
3
π
a
2
4
C.
3
π
a
2
D.
π
a
2...
Đọc tiếp
Cho hình lập phương cạnh a nội tiếp mặt cầu (S). Tính diện tích mặt cầu (S).
A. π a 2
B. 3 π a 2 4
C. 3 π a 2
D. π a 2 3
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD, S là điểm đối xứng với O qua CD’ (như hình vẽ). Thể tích của khối đa diện ABCDSA’B’C’D’ bằng A.
2
a
3
3
B.
3
a
3
2
C.
7...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD, S là điểm đối xứng với O qua CD’ (như hình vẽ). Thể tích của khối đa diện ABCDSA’B’C’D’ bằng
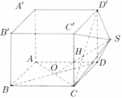
A. 2 a 3 3
B. 3 a 3 2
C. 7 a 3 6
D. 4 a 3 3
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hình vuông ABCD và ABCD. Tính S. A.
S
πa
2
B.
S
πa
2
2
2
C.
S
πa
2
2
D.
S...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hình vuông ABCD và A'B'C'D'. Tính S.
A. S = πa 2
B. S = πa 2 2 2
C. S = πa 2 2
D. S = πa 2 3
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng A.
V
π
a
3
24
B.
V
π
a
3
3
C.
V
π
a...
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
A. V = π a 3 24
B. V = π a 3 3
C. V = π a 3 6
D. V = 4 3 π a 3
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M,N lần lượt là trung điểm của các cạnh A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành 2 phần. Gọi V1 là thể tích của phần chứa đỉnh A, V2 là thể tích của phần còn lại. Tính tỷ số
V
1
V
2
A. 2/3 B. 55/89 C. 37/48 D. 1/2
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M,N lần lượt là trung điểm của các cạnh A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành 2 phần. Gọi V1 là thể tích của phần chứa đỉnh A, V2 là thể tích của phần còn lại. Tính tỷ số V 1 V 2
A. 2/3
B. 55/89
C. 37/48
D. 1/2
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2
9
điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ...
Đọc tiếp
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9 điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là
A. ( P ) : x + 2 y + 3 z + 6 = 0
B. ( P ) : x + 2 y + z - 2 = 0
C. ( P ) : x - 2 y + z - 6 = 0
D. ( P ) : 3 x + 2 y + 2 z - 4 = 0
Một hình lập phương có diện tích mặt chéo bằng
a
2
2
. Gọi V là thể tích khối cầu và S là diện tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng A.
S
V
3
π
2
a
5
2
B.
S
V...
Đọc tiếp
Một hình lập phương có diện tích mặt chéo bằng a 2 2 . Gọi V là thể tích khối cầu và S là diện tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng
A. S V = 3 π 2 a 5 2
B. S V = 3 3 π 2 a 5 2
C. S V = 3 6 π 2 a 5 2
D. S V = 3 π 2 a 5 2




