Các câu hỏi tương tự
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng A.
3
5
4
14
B.
14...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
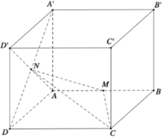
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14
Cho hình lăng trụ đứng ABCD.ABCD có đáy ABCD là một hình thoi cạnh a, góc
BAD
^
60
°
.
Gọi M là trung điểm AA và N là trung điểm của CC Chứng minh rằng bốn điểm B, M, N, D đồng phẳng. Hãy tính độ dài cạnh AA theo a để tứ giác BMDN là hình vuông. A.
a
2
B. a C.
a...
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là một hình thoi cạnh a, góc BAD ^ = 60 ° . Gọi M là trung điểm AA' và N là trung điểm của CC' Chứng minh rằng bốn điểm B', M, N, D đồng phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN là hình vuông.
A. a 2
B. a
C. a 2 2
D. a 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
. Gọi I là trung điểm AB. Mặt phẳng
I
B
D
cắt hình hộp theo thiết diện là hình gì? A.Hình bình hành B. Hình thang C. Hình chữ nhật D. Tam giác
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Gọi I là trung điểm AB. Mặt phẳng I B ' D ' cắt hình hộp theo thiết diện là hình gì?
A.Hình bình hành
B. Hình thang
C. Hình chữ nhật
D. Tam giác
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
2
a
,
A
D
a
,
A
A
a
3
. Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (BMC) bằn...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = a , A A ' = a 3 . Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (B'MC) bằng
A. a 21 7
B. 2 a 21 7
C. 3 a 21 7
D. a 21 14
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Gọi M, N lần lượt là trung điểm của cạnh
A
B
và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và
H
là khối đa diện còn lại. Tính tỉ số
V...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi M, N lần lượt là trung điểm của cạnh A ' B ' và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và H ' là khối đa diện còn lại. Tính tỉ số V H V H '
A. V H V H ' = 55 89
B. V H V H ' = 37 48
C. V H V H ' = 1 2
D. V H V H ' = 2 3
Cho hình lập phương ABCD.ABCD có cạnh bằng a . Gọi O và O lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B C và CD. Tính thể tích khối tứ diện OOMN. A.
a
3
8
B.
a
3
C.
a
3
12
D.
a
3
24
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a 3
C. a 3 12
D. a 3 24
Cho hình lập phương ABCD.ABCD cạnh a. Các điểm E và F lần lượt là trung điểm của CB và CD. Mặt phẳng ( AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thểtích khối chứa điểm A và
V
2
là thể tích khối chứa điểm C’. Khi đó tỉ số
V
1
V
2
bằng A.
25
47...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm E và F lần lượt là trung điểm của C'B' và C'D'. Mặt phẳng ( AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể
tích khối chứa điểm A' và V 2 là thể tích khối chứa điểm C’. Khi đó tỉ số V 1 V 2 bằng
A. 25 47
B. 1
C. 17 25
D. 8 17
Cho hình lập phương ABCD.ABCD có cạnh bằng a, một mặt phẳng cắt các cạnh AA , BB, CC, DD lần lượt tại M, N, P, Q Biết
AM
1
3
a
,
CP
2
5
a
Thể tích khối đa diện ABCD.MNPQ là A.
11
30
a
3
B.
a...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, một mặt phẳng cắt các cạnh AA' , BB', CC', DD' lần lượt tại M, N, P, Q Biết AM = 1 3 a , CP = 2 5 a Thể tích khối đa diện ABCD.MNPQ là
A. 11 30 a 3
B. a 3 3
C. 2 a 3 3
D. 11 15 a 3
Cho hình hộp
A
B
C
D
.
A
B
C
D
, và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là : A. Hình ngũ giác B. Hình lục giác C. Hình tam giác D. Hình tứ giác
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' , và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là :
A. Hình ngũ giác
B. Hình lục giác
C. Hình tam giác
D. Hình tứ giác