Chọn D.

Phương pháp: Phương pháp tọa độ.
Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1


Chọn D.

Phương pháp: Phương pháp tọa độ.
Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1


Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi K là trung điểm của DD' Tính khoảng cách giữa hai đường thẳng CK, A'D
A.a
B. 3 a 8
C. 2 a 5
D. a 3
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Gọi K là trung điểm DD’. Khoảng cách giữa hai đường thẳng CK và A'D là
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 4
Cho hình lập phương A B C D , A ' B ' C ' D ' có cạnh bằng a. Gọi K là trung điểm của DD¢. Tính khoảng cách giữa hai đường thẳng C K , A ' D
A. a
B. 2 a 5
C. a 3
D. 3 a 8
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh bằng a. Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A’ D.
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 4
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
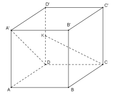
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi K là trung điểm của DD¢. Khoảng cách giữa hai đường thẳng CK và A’D¢ bằng
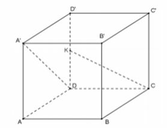
A. a 3 3
B. a 3 2
C. 2 a 3 3
D. a 3
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh bằng 2 a . Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D'.
A. a 3
B. 2 a 5 5
C. 2 a 3 3
D. 4 a 3 3
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi K là trung điểm của DD¢. Khoảng cách giữa hai đường thẳng chéo nhau CK và AD¢ bằng:
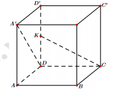
A. a 3 3
B. a 3 2
C. 2 a 3 3
D. a 3
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B′C′ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B′D′ bằng
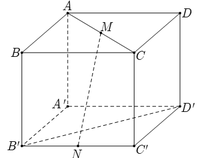
A. 5 a 5
B. a 3
C. 5 a
D. 3 a