Các câu hỏi tương tự
Nhắc lại định nghĩa vectơ không gian.
Cho hình lăng trụ tam giác ABC.A'B'C'. Hãy kể tên những vectơ bằng vectơ A A ' → có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Cho hình lăng trụ tam giác ABCA'B'C' có các cạnh bên là AA', BB', CC'. Gọi I và I'tương ứng là trung điểm của hai cạnh BC và B'C'.
a) Chứng minh rằng AI // A'I'.
b) Tìm giao điểm của IA' với mặt phẳng (AB'C').
c) Tìm giao tuyến của (AB'C') và (A'BC).
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm các cạnh bên AA’, BB’, CC’. Khẳng định nào sau đây là đúng
Cho hình lăng trụ tam giác ABC.A'B'C' có độ dài cạnh bên bằng a. Trên các cạnh bên AA', BB', CC' ta lấy tương ứng các điểm M, N, P sao cho AM + BN + CP = a
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.
Cho hình lăng trụ đứng ABC.A’B’C’ có AB1,AC2,AA3 và BAC
120
o
Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM3BM;CN2CN Tính khoảng cách từ điểm M đến mặt phẳng (ABN)
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1,AC=2,AA'=3 và BAC= 120 o Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM=3B'M;CN=2C'N Tính khoảng cách từ điểm M đến mặt phẳng (A'BN)

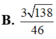
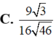
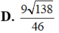
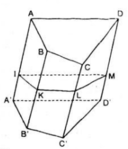
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ
Cho hình lăng trụ tam giác ABC.ABCcó tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc
60
ο
và hình chiếu vuông góc của đỉnh A lên mặt phẳng (ABC) trùng với trung điểm của cạnh BC.a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.b) Chứng minh rằng mặt bên BCCB là một hình vuông.
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A'B'C'có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60 ο và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'.
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông.
Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng Gọi M, N lần lượt là trung điểm của các cạnh AB và BC. Mặt phẳng (A’MN) cắt cạnh BC tại P. Tính thể tích khối đa diện MBPABN. A.
V
3
a
3
32
B.
V
7...
Đọc tiếp
Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng Gọi M, N lần lượt là trung điểm của các cạnh AB và B'C'. Mặt phẳng (A’MN) cắt cạnh BC tại P. Tính thể tích khối đa diện MBPA'B'N.
A. V = 3 a 3 32
B. V = 7 3 a 3 96
C. V = 7 3 a 3 48
D. V = 7 3 a 3 32
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA 4AM, BB 4BN. Mặt phẳng (CMN) chia khối lăng trụ thành hai phần. Gọi
V
1
là thể tích khối chóp C’.A’B’MN và
V
2
là thể tích khối đa diện ABCMNC’. Tính tỷ số
V
1
V
2
A.
V...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA' = 4A'M, BB' = 4B'N. Mặt phẳng (C'MN) chia khối lăng trụ thành hai phần. Gọi V 1 là thể tích khối chóp C’.A’B’MN và V 2 là thể tích khối đa diện ABCMNC’. Tính tỷ số V 1 V 2
A. V 1 V 2 = 1 5
B. V 1 V 2 = 4 5
C. V 1 V 2 = 2 5
D. V 1 V 2 = 3 5